Complex Filter

The previous page 'Complex Resonator' explored how a resonating filter reacts to a single-sample pulse input. Now I want to find out what a complex integrator does with complex sinusoidal input signals. Later on, I will figure out what interesting filter jobs can be done with a complex integrator on a real-only input signal.

To test the complex integrator as a filter, I wrote a separate Max/MSP object. Instead of the user parameter decay time, I reverted to the more direct parameter radius again, because some relations between radius and output amplitude must be examined.

By way of complex test signal, I feed a computer-generated cosine and sine wave in the respective inputs of the complex resonator. Because a (complex) sinusoid has more energy than a single sample pulse, it can be predicted that the resonator will produce an increased output level. The output amplitude can be easily computed by doing Pythagoras on the real and imaginary output.

In a first test I set radius 0.9, and let the input frequency match the filter center frequency at 200 Hz:

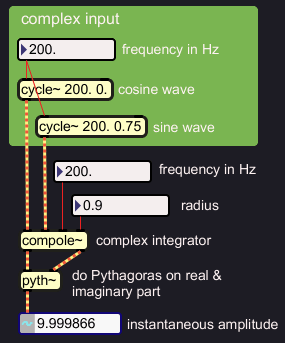Oops, the output has almost amplitude 10, while amplitude 1 is unity gain. I am happy that I did not play this over my speakers yet. Increasing the radius, leads to further growth of the output amplitude. Here are some values:

radius 0.9      amplitude 10
radius 0.99     amplitude 100
radius 0.999    amplitude 1000
radius 0.9999   amplitude 10000

The input amplitude seems to be magnified by:

Let me first do something about these crazy amplitudes. If I normalise the input by applying the inverse of the observed gain factor, I expect to keep the output within the limit of unity gain:

This does the job indeed. The input sample values are multiplied by a factor 1-radius. In the above example, that is 10, and for larger radiuses it can mean a substantial input attenuation. Still the output grows to a stable amplitude around 1 everytime. That is a remarkable phenomenon. For ease of use, I incorporate this normalisation in the object.

Now that the complex integrator input is normalised, filter characteristics can be checked. To visualise the filter effects, I feed complexified noise in, and plot a complex spectrum of the output. I use linear scales for amplitude and frequency, and an example with a fairly high filter center frequency:

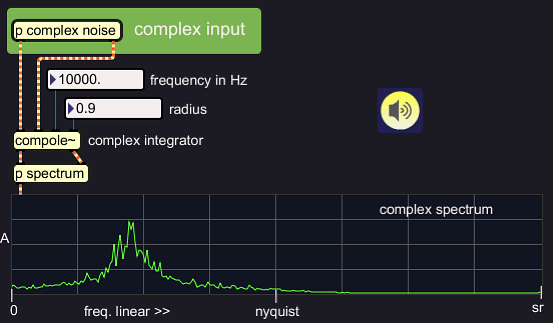The complex integrator is a bandfilter. Increasing the radius, for example to 0.999, will make the band narrower:

At high radius settings, integration can make very narrow bandfilters. But there is a down side. We have seen how the input must be attenuated according to radius setting; the normalisation factor in the above example is 0.001. If the input is so much reduced, it must also be the case that the integrator needs some time to rise to it's full output level. Even if the input sound has a fast attack, the filter will not be able to follow that. Below is an example for radius 0.999. The signal input and output of one phase are shown:

With 1-radius input attenuation, the rise time is of the same order as the decay time, about 25 milliseconds in the above example. This is best observed with a square wave input, which is equivalent to a framed DC input:

The slow rise time in narrow resonating filters is bothersome. Any fast attack will not make it through the filter. It would be nice if we could make that filter work a bit faster. Well? This can be done, actually.

Below, I use three complex filters instead of one. This means, for every sample moment, three complex multiplications are done instead of one. It is a way of oversampling. The filter effect of radius 0.999 is now done with radius 0.99 for each filter.

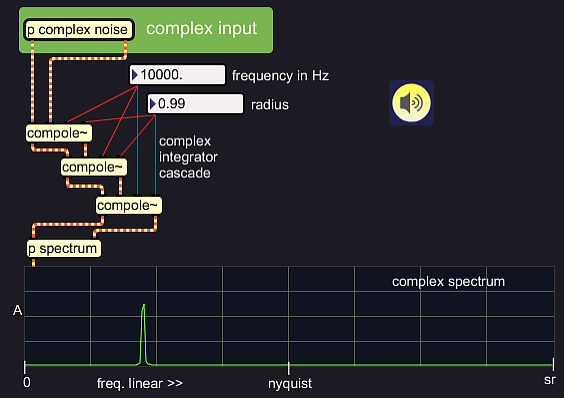Checking the rise time of an input frequency at the filter's center frequency, shows a much faster rise for the cascade indeed:

single integrator, radius 0.999

cascade, radius 0.99

positive and negative frequencies

I did not tell how I complexified noise before feeding it into compole~. To be honest, I still have to find out how to make a complex signal. In the meantime, I use Max/MSP's hilbert~ object which does the necessary 'Hilbert Transform'. It has sets of allpass filters with a phase deviation amongst them, 90 degrees for most frequencies, exept the lowest frequencies and the highest octave. I would think that Hilbert Transform should produce positive frequencies exclusively. Below, you can see that hilbert~ produces negative frequencies. This has confused me many times. Anyway, positive frequencies could be produced by sign-flipping the imaginary output phase.

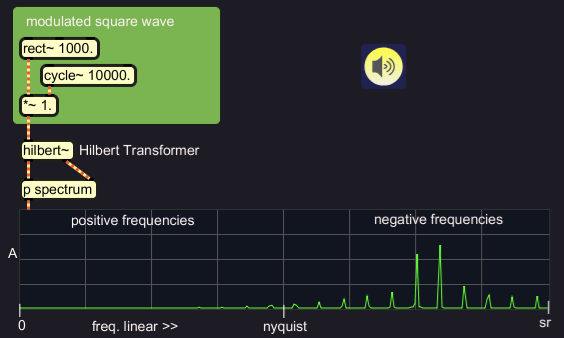Since Hilbert Transform can make complex signals with positive or negative frequencies exclusively, it is also possible to do both, but with different content, and mix these down into one complex signal. I have done that in the example below, to produce a weird demonstration spectrum where the frequencies above Nyquist are not aliases of those below Nyquist. The filter radius is at 0 to show the full output:

The complex integrator can distinguish positive from negative frequencies, so it is now possible to suppress positive frequencies for example, and let a band of negative frequencies pass through:

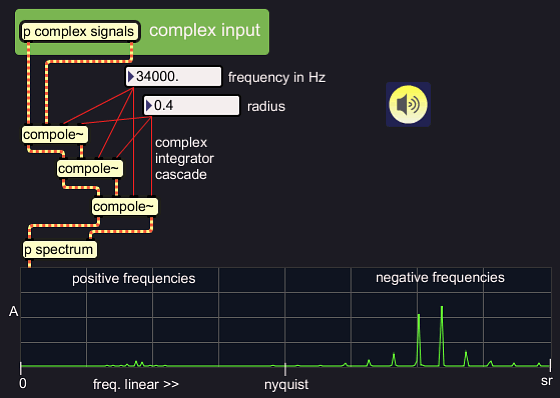At the moment, I have no specific purpose for such single sided filtering. But I find it so cool, I just wanted to do the illustrations.

It is by the way no problem to feed a real signal in the complex integrator and filter this:

When we want to hear the filter output, we must choose one of the filter output phases, since we can not listen to a complex signal. When a real signal was sent in the filter, there seems to be a difference in the spectra of the outputs. I set the radius value low so it can be better perceived. In the first case, the real output is taken:

When the imaginary output is taken, the low frequencies are more pronounced:

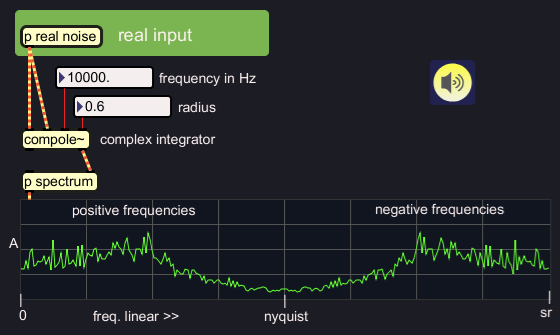This phenomenon is reminiscent of the state variable filter, where it is exploited to produce hi pass, low pass and band pass from one filter process. With the complex integrator, the effect can not be fully exploited. If a real signal is sent in a complex integrator cascade, the spectral difference between real and imaginary output at the last filter is gone. How come? The integrators tend to make a real signal complex. And for complex signals, the complex integrator is a plain band pass filter at both outputs.

If a complex integrator tends to make a real signal complex, can it not be used for Hilbert Transform? That is what I had been hoping for. Unfortunately, it only works well with high radius settings, which means, narrow filter bands. Here is an example. The circle on the x-y scope demonstrates the orthogonality of the phases:

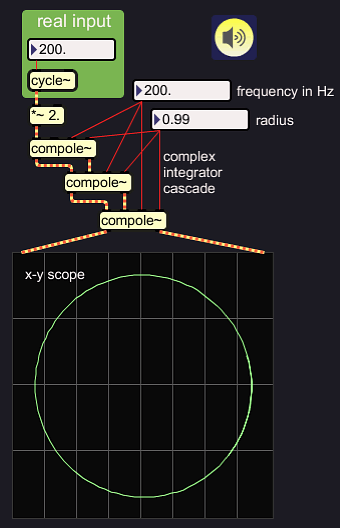At high center frequencies, the radius setting can be lower, and still a precise complex signal comes out:

It is even possible to transform a 15 KHz signal from real to complex, that is something which the hilbert~ object can not do.

This opens up one interesting perspective. If you would need to do a constant Q filter bank for any reason, you could have complex outputs at little extra cost. But what if you want a complex signal without the filter effect? I have now written so much on complex signals, I really feel urged to figure out how Hilbert Transform can be done, and do a solid illustrated documentation of that.