<<home <<previous next>>

Invertible FFT

I have learnt, and echoed, that reversal in time domain is equivalent to conjugation in frequency domain. When I tried to exploit this equivalence for the first time in a practical application, a complication for discrete time presented itself. I could have known that before, had I better inspected my own illustrations. The following is copied from my page Fourier Matrix:

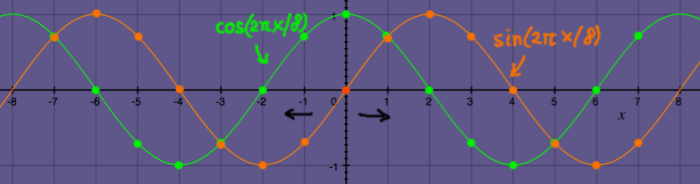
With that plot I illustrated how the conjugate of a complex sinusoidal function could be derived by going in the reverse direction, starting from zero. But look what happens when we reverse a N=8 complex array containing the fundamental sinusoid:

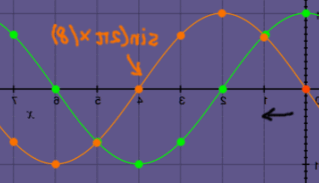These are not exactly a conjugate pair. It is phase-shifted, by one sample. If I compensate for this phase-shift, it looks better:

I shifted the illustration such that the original samples 0 till 7 coincide with sample 1 till 8 of the flipped picture.

One sample, is that such a big deal? For an inverse FFT, I tried using a reversed array of complex roots of unity, instead of a conjugated array. That is how I encountered the problem. The effect can hardly be overlooked. Below is an example for N=64. The left picture is with the roots conjugated, while the right picture is with the roots array reversed:

I am still digesting the implications of this one-sample discrepancy. Anyway, I was looking for a bitwise method of inverting an FFT function, such that it can be used for both directions. For this case, it is not so problematic.

Recall that only half a cosine and sine function are needed for the twiddle factors. Below is an impression of that. For the inverse FFT the second half of the function points could be used, reading them reversed and with a one sample shift. Since we are the creators of the arrays, we are free to add one sample, but it is not even necessary since we normally skip twiddling in case of identities.

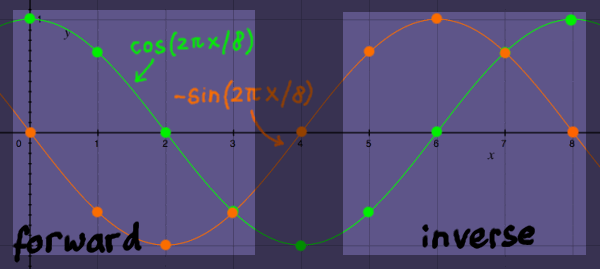I did code for an invertible FFT function using the reversed array with complex roots of unity. But later I have abandoned this, because there is a better option. Since we can organise the arrays in any fashion that suits our needs, I chose to interleave them in such a way that the indexes for the inverse FFT need not be read in reverse direction, but only shifted by one position. Here is an impression of cutting, stretching, reversing and interleaving:

The even indexes are for the forward transform and the odd indexes for the inverse. We already knew there is only one difference for the inverse twiddle factors: the sine part has opposite sign. It could be more advantageous to just use the half functions and make the twiddle code conditional, specially for systems with small (cache)memory. But since I am determined to find a bitwise alternative, I will continue with that. Here is a function for interleaved complex roots of unity:

void rootsofunity(double *realtwiddle, double *imtwiddle, unsigned int logN)
{
double pi = 3.14159265358979;
unsigned int n, N;

N = 1<<logN;

    for(n=0; n<N; n+=2)
    {
       realtwiddle[n] = cos(pi*n/N);     // roots for n=even, forward transform
       imtwiddle[n] = -sin(pi*n/N);

       realtwiddle[n+1] = cos(pi*n/N);   // roots for n=odd, inverse transform
       imtwiddle[n+1] = sin(pi*n/N);}
    }
}

In the function definition, a boolean argument 'invert' is included which shall be true for inverse FFT, and false for forward FFT.(#include <stdbool.h> in the header). The boolean is used as a switch for a one sample offset. This needs to be done only once per FFT stage, as the offset is kept during decrement of the rootindex variable.

The direction of the rotations is now dependent on the 'invert' argument. A simple true or false invokes more bitwise logic, and does it's work without conditional expression. Admittedly, that is a rather futile detail. Specially since it does not seem to save one microsecond. Bah...

That was for the twiddle factors. The normalisation in the inverse FFT also needs special attention. I have done a page on normalisation matters, and I will not repeat the considerations here in detail, but just use 1/N normalisation in the forward transform.

void fft(double *real, double *im, double *realtwiddle, double *imtwiddle, int logN, bool invert)
{
    unsigned int N, even, odd, span, rootindex;
    unsigned int phase;         // angle of primitive root of unity
    unsigned int rootmask;      // for modulo N computation and for direction
    double temp, norm;


    N = 1<<logN;
    norm = 1./N;                // 'normalisation' factor
    rootmask = N-1;
    phase = 1;                  // phase bias because of interleaved roots of 1

    for(span=N>>1; span>1; span>>=1)
    {
        phase <<=1;                             // update in every FFT stage
        rootindex = (N-phase) ^ invert;         // initialize in every FFT stage

        for(even=N-span; even;)                 // iterate over the dual nodes
        {
            even--;
            odd = even|span;
            even = odd ^ span;                  // iterate over even blocks only

            temp = real[even] + real[odd];
            real[odd] = real[even] - real[odd];
            real[even] = temp;

            temp = im[even] + im[odd];
            im[odd] = im[even] - im[odd];
            im[even] = temp;

            if(rootindex)                     // rootindex[0] has an identity
            {
                temp=realtwiddle[rootindex]*real[odd]-imtwiddle[rootindex]*im[odd];
                im[odd]=realtwiddle[rootindex]*im[odd]+imtwiddle[rootindex]*real[odd];
                real[odd] = temp;
            }
            rootindex -= phase;                 // decrement rootindex
            rootindex &= rootmask;              // modulo N computation

        } // end of loop over nodes

     } // end of loop over FFT stages, except last one

     invert = !invert;          // invert the boolean for faster check

     for(even=N; even; )    // last FFT stage including normalisation
     {
        even -= 2;                // attention, decrement at unusual place
        odd = even|1;

        temp = real[even] + real[odd];
        real[odd] = (real[even] - real[odd]);
        real[even] = temp;

        temp = im[even] + im[odd];
        im[odd] = (im[even] - im[odd]);
        im[even] = temp;

        if(invert)                // recall that invert = !invert
        {
            real[even] *= norm;   // 'normalisation' only in forward transform
            im[even] *= norm;
            real[odd] *= norm;
            im[odd] *= norm;
        }
     }
     // end of last FFT stage

} //end of function

One obvious test for code like this, is to have it inverse-transform it's own result. But in order to do so, we need a bitreversed sorting inbetween, and after the inverse transform. The algorithm is for input in natural order and output in decimated order. To be honest, I completely forgot about the whole decimation thing, while developing my freaky bitwise FFT inverter. That is stupid eh? It is time to figure out the bit reversal. See the next page.

^top <<home <<previous next>>