Sinusoids Correlation

On the previous pages the amplitudes of sine, and cosine, were illustrated as being 2^-(1/2), or one over the square root of two. Which is around 0.707. Now I will use sine and cosine as correlation vectors, like it can be done in Fourier Transform. For me at least, there were a couple of surprises.

Below, I use cos(2*pi*x) as a correlation vector. Can I find 0.8cos(2*pi*x) by correlating this with cos(2*pi*x)? The inner product is the result of this correlation. It is the integrated area over the interval [0,1]. It seems to be 0.8/2=0.4. Apparently, only half of 0.8cos(2*pi*x) is found. Is that coincidence?

Here is another example where I try to find the correlation of 0.6cos(2*pi*x) with cos(2*pi*x). The integrated area is 0.6/2. Again, only half of 0.6cos(2*pi*x) is found.

One explanation for this is that the other half of the correlation is in the conjugate. A real signal of period (2*pi*x) could be described:

0.5[cos(2*pi*x)+isin(2*pi*x)] + 0.5[cos(2*pi*)-isin(2*pi*x)]

When we do correlation with both of the conjugated vectors, we would find 2 times 0.3 and it would be complete. But not all transform types use complex conjugates. It would be nice to have an alternative explanation as well.

Computing correlations means computing inner products. A signal squared is also an inner product, and shows the energy in the signal. A cosine has energy 0.5. Correlation of cosines will result in a coefficient which is proportional to 0.5, and not to 1. Consider the figure below. 0.6 times cosine-squared would result in the same inner product: 0.3.

Following this argumentation, we could do correlations with cosine of non-integer period, like cos(3*pi*x). Such functions are used in Discrete Cosine Transform, where complex numbers are absent.

And here is the equivalent inner product for 0.6 times cos(3*pi*x) squared:

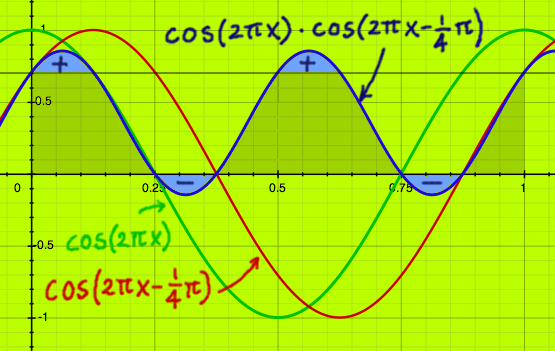
The question is, what will happen in case of phase-shifted vectors. Below, I delayed one cosine vector with 1/8th period before doing the correlation. The inner product is half the area under 0.7, according to the figure. I have a feeling that this could be one over the square root of two, more precisely.

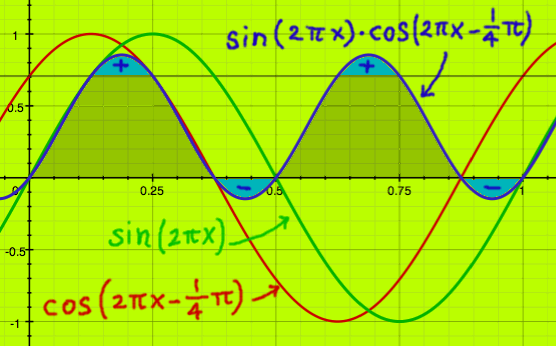
When the delayed cosine is correlated with sine of the same periodicity, 0.7/2 is found as the inner product again.

Correlation with negative sine results in a different sign:

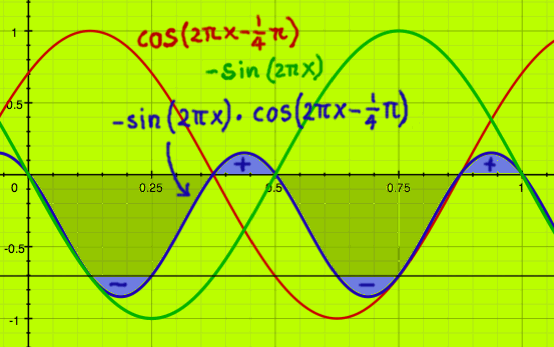I was using parts that belong to the complex conjugates at (2*pi*x).The function cos(2*pi*x-1/4*pi) can be described:

There is in total 0.5^1/2 cosine part in it, and 0.5^1/2 sine part. These parts are not amplitudes! Because sine and cosine have amplitude 0.5^1/2, the amplitudes of each part would be 0.5^1/2*0.5^1/2=0.5. The combined amplitude would be:

That is something we already knew, because the input was a full cosine. But if you have a real signal with unknown content, correlations like the above described could serve to find the amount of sine and cosine of a specified periodicity in it. And from that, the amplitude and the phase could be computed, if needed.

There is one more correlation plot that I want to show. It is cosine with periodicity one-and-a-half, and a phase-shifted version thereof. Here again, we see the 0.5^(1/2)/2 inner product.

In this case there is not a complex vector, let alone a conjugate pair, to complete the picture. In discrete transforms, cos(3*pi*x) will have an alias. The alias will correlate another 0.5^(1/2)/2. Together that makes for 0.5^(1/2)cos(3*pi*x-1/4pi). The rest of the correlation will be spread over other frequencies. It is not something that can be nicely plotted.

But I do not think that complex vectors are superior for this reason. In real life, frequencies in correlated signals rarely coincide exactly with the frequencies in a transform matrix. Complex vectors spend double attention to each frequency, at the price of a double distance between frequency points, when compared to the discrete cosine set.