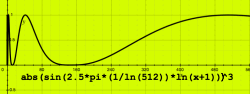Parametric Fourier Filter

I have always been a fan of Cool Edit's built-in Fourier filter, which can do extreme yet quite precise filtering. For some time I daydreamed about making a similar filter for real-time audio processing. The curve in my filter should be controlled by a few parameters, and not by drawing innumerable points on the computer screen. The key to a musically effective multiband filter is a logarithmic distribution of center frequencies and bandwidths, which is better set by mathematical formulas than by eye and hand.

When starting out, I was still unaware of some issues related to spectral processing, notably the resolution/latency trade-off. Soon, it became clear that the linear character of a DFT spectrum output would not allow a 32-band filter, if at the same time an acceptable latency for real time purposes were to be retained.

The Fourier filter can not replace a time domain filter (bank) in all situations. While learning about these limitations the hard way, by trial and error, (because I am too stubborn to take wise people's words for granted) I worked out my parametric Fourier filter and made the best of it, given the conditions. The result so far is a relatively light-weight and flexible routine, linking the appreciated sound characteristic to a surprising ease of handling. Let me reveal some details of the concept.

The essence of my filter's amplitude spectrum is a plain logarithmic curve. On the left, part of the natural logarithm curve ln(x) is plotted. For any base logarithm, x[0] always has y=-infinity and x[1] has y=0.

A very famous one is the base-2 logarithm. It is not on pocket calculators or in the standard C-library. But it is easily computed with 2log(x)=ln(x)/ln(2.). I have set black dots at the base-2 logarithms of 1, 2, 4, and 8.

Base 2 or radix 2 is the number system for computers, the binary system, so base 2 exponents and logarithms are implicitly used all the time. It also happens to be the 'octave-logarithm', describing how frequencies relate to octaves in pitch perception.

Spectrum coefficients represent frequencies in terms of harmonics of the DFT fundamental. The fundamental is a sinusoid with one cycle fitting exactly in the analysis frame. Coefficient x[0] represents the DC component, and x[1] represents the DFT fundamental. It's frequency in Hz depends on the DFT size and samplerate, but coefficient x[2] is always the second harmonic, being the octave of x[1]. x[4] has another octave, then x[8], x[16], x[32] and so on. The pattern is, that the octaves are at x[2ⁿ], n being an integer. Inbetween coefficient x[0] and x[1] are infinitely many more lower octaves, none of which can be represented as such. An impression of that is plotted below. The black dots indicate spectrum coefficients and the continuous line shows peaks at octaves.

From this, it is clear that filterbands smaller than octaves are impossible in the lowest frequencies region. Higher up, the pitch resolution gets better, and it is possible to create narrow peaks at octave intervals:

Upward from bin x[30], the resolution would allow isolated bands at third-octave intervals, like plotted below:

Specially the third-octave bands make a multibandfilter 'sing' rich and harmonically, but larger intervals have interesting characters as well. By the way, a time domain third-octave filter with all it's bands up is not supposed to sing at all, but due to phase cancellations, they have that tendency, which has become an appreciated sound in itself. With Fourier filtering this can be pushed to the extreme, but the lowest bands are not controlled with precision and tend to just disappear in many cases.

I could now compute what FFT size is theoretically required to do such extreme filtering. Say I want to control third octaves from 40 Hz up with fair precision. My first guess is that a 2¹⁵ point FFT would do. Let's see: 2¹⁵ is 32768 points. With samplerate 44k1 this makes an FFT fundamental of 44100/32768 = 1.3458 Hz. Harmonic 30 is at 30*1.3458 = 40.3 Hz in that case, and that is where the filtering would start being more or less precise. A 32768 point FFT is not so extravagant in itself and may take a millisecond CPU time, but all these samples have to be collected before a frame can be processed. That takes 743 milliseconds! Blah....

Now you see where the bottleneck is with spectral filtering. I could not find a compromise that can pair acceptable latency to the precision needed for my extremest filtering desires. I will have to switch FFT sizes according to the purpose, and not use the third octaves (or the Fourier filter at all) when timing is crucial. In practice, I found a 2¹³ point FFT sufficient for needle-thin bands at third-octave intervals. I typically use wide-band noisy input for such filtering, and the lower bands seem fairly well preserved. A 2¹⁰ point FFT can not do this, but will serve for most other purposes. This FFT length can also be abused for extreme filtering, but it may introduce artefacts, which are welcomed in some cases and abhorred in others. More on artefacts later, let me now illustrate the mathematical operations that I use to construct multiband filter spectra.

Indexing starts at x[0] but I want to avoid the  minus infinity result of ln(0.), which would propagate through all subsequent operations and might lead to Not A Number somewhere. I simply add 1 to x before taking the logarithm. This is a distortion of the perfect logarithmic flow, but it also makes the disappearing-band effects less systematic, which is an advantage.

The logarithmic curve will supply the phase arguments for a (co)sine function, to create a logarithmic sweep. In order to normalise the sweep somehow to the FFT size, the logarithmic curve is first multiplied with pi/ln(FFTsize/2). The  FFT's half framesize equals the number of spectrum coefficients, with the conjugates left out. The multiplication does not take away the logarithmic character of the curve.

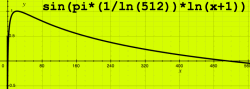
Here is the example for one filterband on a 512 point spectrum. The asymmetric appearance matches the logarithmic nature of pitch perception.

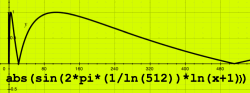
Multiplying the one-band log curve with 2 before computing the sinusoid, makes the sine rotated over a total of 2 pi within the 512 point spectrum.

With the abs() function the sweep is rectified, and exactly two filterbands result.

By simple multiplication of the initial log curve I could effectuate any desired number of filterbands. It need not be an integer number. Here I have set 2.5 bands.

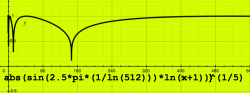Raising the complete function to a power alters the slopes. A power inbetween 0 and 1 is actually root extracting and makes less steep slopes, till the point of a flat spectrum at power 0. Be careful not to set a power below zero!

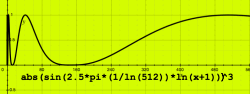
Powers above 1 make steeper slopes. Here is the rectified sweep raised to the power of 3.

Of course I also want to control the center frequency of the filterbands. This can be done by simple phaseshift of the sweep. Very conveniently, the bandwidth varies with position and it seems to retain it's Q factor.

The constant Q works because the sweep originates from a logarithmic curve. The plot here illustrates how a -pi/2 phase shift makes dips exactly at the positions of the peaks in the original function, and vice versa.

Finally, I multiply the sweep with factor 1.5 and clip at y=1. Each band will then get a flat region, which gives them better definition.

The passive filtering process generally reduces the output energy, and with narrow peaks the loss can be substantial. Therefore I implemented a partial amplitude compensation, linked to the power function. The integrated area under the sweep diminishes inversely proportional to roughly the square root of the power to which the sweep is raised. A power of 16 would theoretically require a factor 3.5 amplitude compensation, and a power of 64 (my maximum) require a factor 7 compensation. Due to perception issues and limited headroom, that is way too much in practice. For now, I have set a maximum amplitude gain factor 2, which may be a little conservative.

After some experimenting, I decided my filter could do with three user parameters:
- number of filterbands (from 1 to 32)
- Q factor adjustment (starting at flat spectrum)
- frequency position of filterband(s)

All settings in the examples below are done with just these parameters:

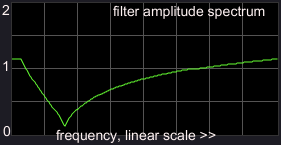
(1) almost flat spectrum

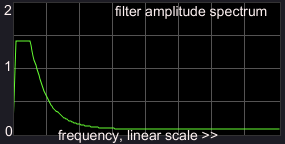
(2) increased Q factor

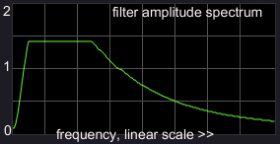
(3) further increased Q factor

(4) frequency shift, Q factor retained

(5) more filterbands

(6) frequency shift, Q factor retained

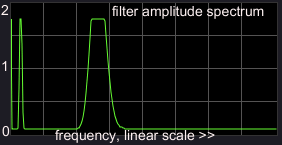
(7) further Q factor increase

(8) more filterbands

on artefacts

Creating steep slopes in a filter spectrum can introduce artefacts in the filtered signal, as I could clearly hear. How come? I think it is because frequencies in a signal are never correlated by one single Fourier coefficient, but the correlation is always spread over more neighbouring bins. Zeroing out part of these correlation coefficients and leaving the others, will create frequencies which were not in the input signal.

For a short while, I was seriously disappointed by the poor results of Fourier filtering. Then I remembered about FFT window types influencing the spectral smearing character. I tried overlapping 4 FFT frames instead of the regular 2 frames. The extra overlap turned out to be more decisive than the window type. This resolved my problem to a large extent, at the price of extra FFTs. But FFTs are not so expensive at all. At least I could now use the Fourier filter with more extreme settings for delicate signal types like voice processing. Later on, I have done minute experiments to find the best windowing options for the
Fourier filter. It is documented on the page FFT Windowing & Filtering.

I prototyped the Fourier filter as a Max/Msp patch. The patch is extensively commented on the next page, Fourier filter in Max/Msp.