Pitch Shifting

I have just started learning about pitch shifting, and built my first pitch shifters in Pure Data object classes. This page will be dedicated to illustrations which pinpoint at typical bottlenecks of the topic.

Expanding or compressing a signal on the time-axis is a sure way to alter pitch. All frequency components are slowed down or sped up with the same ratio, and this will preserve their harmonic relations. This happens for example when playing a tape at slower or faster speed. Here is a visual impression of slowing down a waveform:

original wave

the same wave played at 3/4 of the speed

Time duration of this slowed down wave is extended to a factor 4/3, the inverse of the speed factor. In case such stretching is done in digital domain, samples are inserted to produce the longer signal length (upsampling).

In many practical situations however, we want time stretching OR pitch shifting, and not both. Time stretching is popularly understood as a change in time duration with preservation of pitch. Pitch shifting is then the opposite: a change in pitch without altering the time duration. While it is still clear what time duration means in this sense (the length of a played sound expressed in seconds or milliseconds), what is actually pitch? The fundamental frequency of a harmonic sound is called it's pitch. Does it mean that inharmonic sounds and noises can not be pitch shifted? Possibly. Anyway, a signal's period or fundamental frequency (if present or expected), should be the elementary unit of concern, as it transfers the pitch sensation.

Pitch shifting is in fact a combination of time stretching and up- or downsampling. Let's first look at an ideal case of time stretching. The original signal from the above example will be stretched to 4/3 of it's length, while preserving the pitch. By coincidence, this can conveniently be done by adding one period:

original wave

the same wave time-stretched to 4/3 of it's length by adding one period

In this time-stretched wave, the time duration is expanded while the pitch is preserved. Subsequently, the time-stretched wave can become pitch-shifted wave by reading it at faster speed. In digital domain this means leaving out samples, downsampling:

time-stretched-and-downsampled wave: raised pitch

With respect to the original wave, the length is retained while the pitch is raised. Here is the original wave once more for comparison:

original wave

It may be confusing that a raised pitch is associated with an expanded time duration and also with downsampling. That is just how it is. The opposite is also true: to lower a pitch sensation, you will need to take away some of the original sound's periods, and then upsample. Why not do an illustration of that as well. Here is the original wave 'time-stretched' to 2/3 of it's length (it has shrunk rather, but that is not part of the terminology):

 
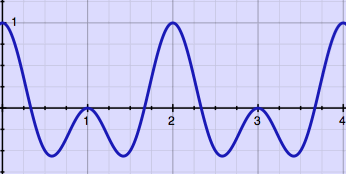wave reduced to 2/3 of it's length by cutting one period

Now upsample this wave till it has the original length, and the effect is a lowered pitch:

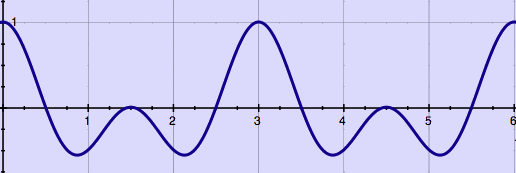time-reduced-and-upsampled wave: lowered pitch

From these examples, it becomes clear that pitch shifting is a matter of taking away samples at some points and adding in samples somewhere else. The net result has identical size, but the trick is to remove and insert at the proper places. Time stretching is a matter of removing or inserting larger sections while keeping periods intact. Resampling is a matter of removing or inserting samples as spreaded and smooth as possible, while expanding or contracting the periods.

I have illustrated that time stretching should preferrably be done by adding or removing full periods, but this is not always possible. Some signals, or regions in it, are not periodic. Even when a signal is periodic, finding and using that information may be troublesome. In real life, pitch shifting is as easy as folding a sphere from a piece of cardboard. Without decent analysis, adding or removing portions of the signal could look like this:

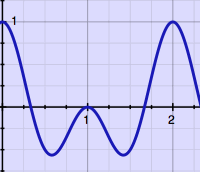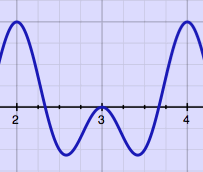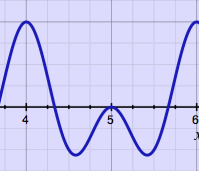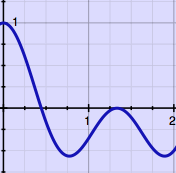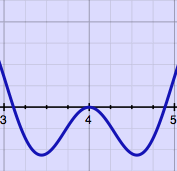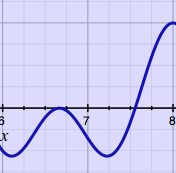Such microscopic cut & splice technique requires at least some amplitude crossfading, to avoid clicks at the joints. I found it fun to learn that electro-mechanincal machines for time stretching and pitch shifting were already invented and produced decades ago.

rotating tape heads

One typical situation where tempo and pitch must be controlled independently, is when recorded radio interviews must be sped up, while the pitch of the voices should remain unaltered. Around the 1960's, the Springer Tempophon with rotating tape heads was developed, and could do such jobs. Several composers, notably Stockhausen, were fascinated by this machine and used it in electronic composition.

The rotating tape heads read the signal at a speed independent from the tape playback speed. The tape speed relative to the machine determines the time duration, while the playback head speed relative to the tape determines the pitch. The heads can move along with the tape direction for lower pitch, or move in the opposite direction for higher pitch. Six tape heads in a drum were used in this mechanical construction. I have never seen a Tempophon with my own eyes, but from descriptions I derived it's working principle. Here is a graphical impression:

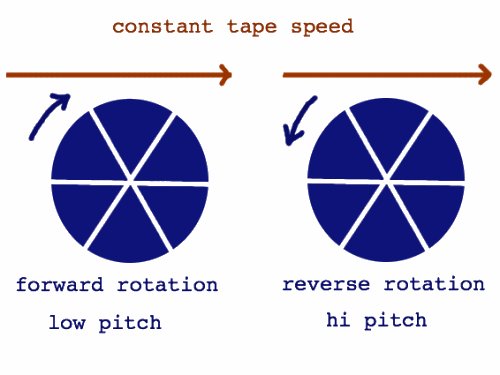It is comparatively simple to emulate a basic rotating tape head machine in digital domain. Since there are no physical constraints forcing virtual tape heads to be round, only two of them are needed, instead of six. Below, it is done as a Pure Data patch:

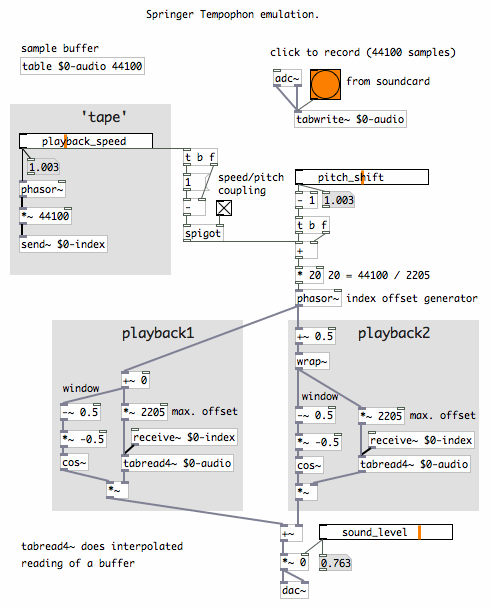The signal buffer is read by two reading objects (tabread4~). Reading can be done at fractional (= slower or faster) speed. An index represents the 'tape position'. The two 'playback heads' have fluctuating offsets from this index, in alternating phases. These phases have overlap, so most of the time you hear both playback heads. The offset fluctuates linearly between zero and a defined maximum. The offset maximum is 2205 samples in the patch, but that could have been a different amount, like 1000. The offset maximum is sort of equivalent to the distance between playback head centers in the rotating drum.

It is also possible to skip variable playback speed and do realtime pitch shifting on an input stream, using a delay with two taps reading at variable speed. Below is a simple Pure Data patch for doing that. For simplicity, the maximum delay time is fixed again, to 50 milliseconds:

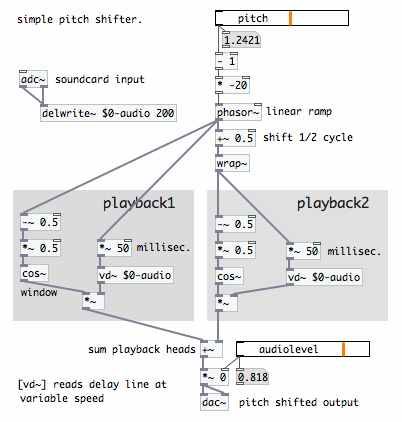The playback outputs are subjected to smooth amplitude regulation, very similar to the method of window and overlap used in Short Time Fourier Transform. Signals are read in overlapping frames while being multiplied with a window function, a 'raised cosine' in most cases. I have copied the following graph from the page 'window & spectral filtering' to illustrate the window and overlap principle:

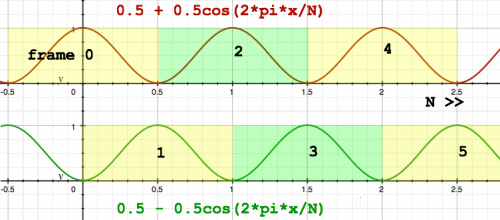overlapping frames with Hann windowing

In the case of Short Time Fourier Transform, the input signal is normally read at unity speed, and window & overlap is only required to relieve the 'boundary effects'. Details of these effects are illustrated on the forementioned page. The sum of windowed and overlapped input frames is identical to the input signal in the case of Fourier Transform. Here is an impression:

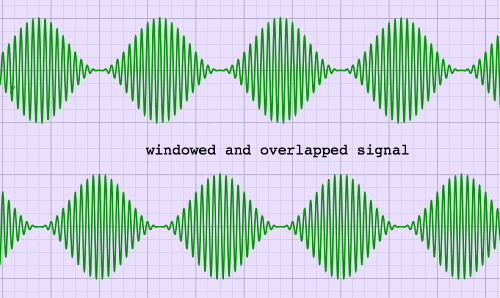With the rotating tape head principle, things are sligthly different. Although the sudden jumps of the frame stitches are now at the window's zero points, the phases in the two playback signals do not necessarily coincide. That is because the frames were resampled at a speed different from the original. Very few frequencies will be exactly in phase, and the rest will be out of phase to some degree. This results in phase cancellations which are prominent in the region of maximum overlap. The most unfavourable phase condition is with the window size being an odd multiple of an input frequency. Here is an example:

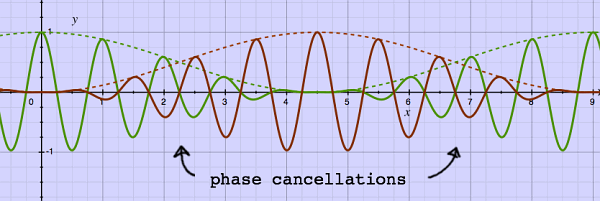The window type makes a difference for the overall result. For Fourier Transform, the Hann window is one of the favourites. The sum of overlapping Hann windows is always a constant. For a Tempophon emulation with it's phase-incoherences, we may prefer another window function. When two signals with independent phase relations are summed, the magnitude is not doubled, but increased to 1.4 instead. This holds for the pitch-shifted frames as well. Therefore, when using Hann windows, there are overall sound level dips at the locations of maximum overlap.

Positive sine windows do not sum to a constant, but produce peaks at the locations of maximum overlap, and these peaks do exactly compensate for the statistical loss of energy caused by phase cancellation. It is the same amplitude curve as found in the crossfader section of a DJ mixer. Here is a plot, showing overlapping sine windows and their sum:

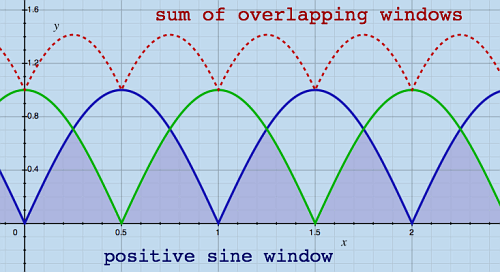This window type produces less overall amplitude modulation when overlapping unrelated phases, therefore it is better suited for the Tempophon emulator. Notice however, that it will produce more amplitude modulation when phases happen to coincide. Thus, amplitude modulation is not eliminated with this window type, only statistically reduced.

Because the frames were taken at different moments in time, overlap areas actually present repetitions, smoothed by the window functions. Apart from spurious modulation, a general comb-filter effect is perceived. Specially with pitch factors above 1, it has the acoustics of a small room with tiled walls. I want to return to the Hann window for a moment, because this window type has relatively little overlap area:

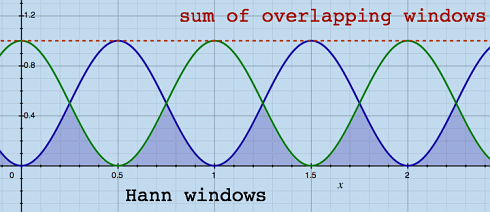With less overlap area, there is also noticably less comb filter effect. Is there not a window type combining the good aspects of both, while leaving out the disadvantages? I was thinking of something like this:

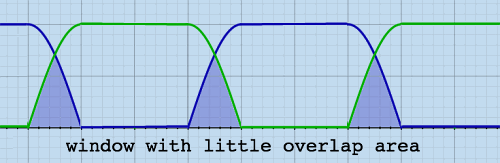This fantasy window is not a mathematical function, and I have partly drawn it by hand. But the crossover region has sinusoidal curves again. This window can be constructed in parts from mathematical functions. The window has 6/6 parts, and is non-zero over 4/6th of it's periodicity:

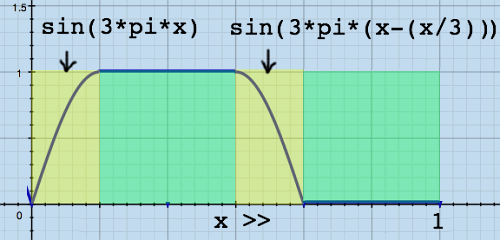I have built the delay lines and two different windows into one Pure Data object [tempophon~], to check the effects. Below, you can see typical modulation patterns resulting from the window types. Although the magnitude dips are equally deep in both cases, the minimum-overlap window leaves a larger area untouched. This reduces the 'echoic chamber effect' somewhat. At the same time it creates extra (but not per se louder) modulation frequencies because of it's more complex shape.

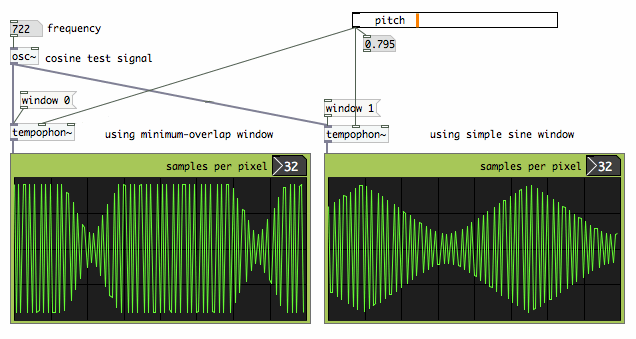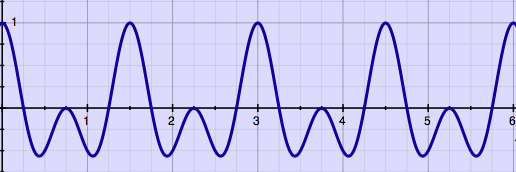
So far I am demonstrating and stressing the most problematic frequencies everytime, but there are also frequencies which come perfectly steady through the pitch shifter. The Tempophon emulator is a 'dumb' pitch shifter, it does not try to tune it's process to the input frequencies. With the above window types, it is even the case that when a frequency comes through unmodulated, it's first overtone would suffer the heaviest modulation. Here is an illustration:

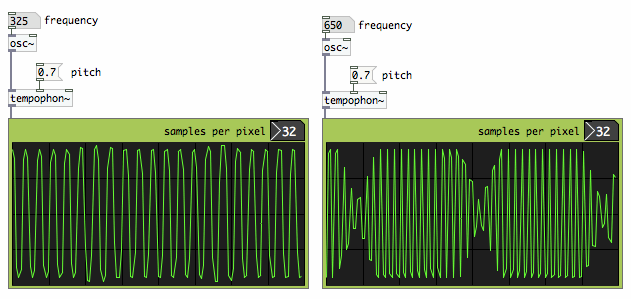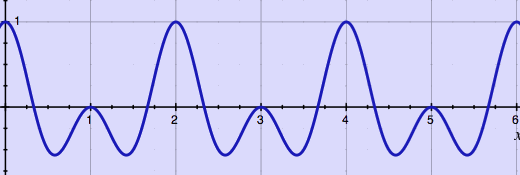
Allmost any sound material will be degraded by this simple pitch shifter process. Due to unconditional processing, and the window type being optimized to inconsistent phases, harmonic sounds will be affected as much as any other sound. Below is a typical result plotted for a harmonic test signal:

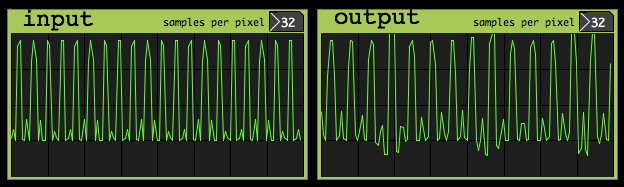sum of two harmonics transposed with pitch factor 0.7

To get better results, the signal content must be analysed in some way, and the microscopic cut & splice actions should match the signal's waveshape whenever possible. Several time domain methods exist, each analysing the signal in a different way. Unfortunately, such methods are way more complicated than the basic window & overlap principle itself, and they can not be reproduced with a couple of Pure Date objects.

PSOLA, Pitch Synchronous  Overlap Add, tries to find the pitch of the input signal, and apply a grain size of 2 or 4 times the fundamental frequency. Finding a signal's pitch is a hazardous job. Polyphonic sounds or sounds with 'missing fundamental' can give erratic analysis results.

WSOLA, Waveform Similarity/Synchronized Overlap Add, does not need knowledge about fundamental frequency or harmonic content. Instead, it keeps the grain size fixed, while the best locations for overlap are found by moving the grains and computing the cross-correlation. Like playing around with jigsaw-puzzle pieces and finding out how they fit best. The method was proposed by Verhelst & Roelands, see for example [this link].

Olli Parviainen has published an open source C++ library for time stretching and pitch shifting, using a WSOLA-like stretching algorithm. This is the SoundTouch library, incorporated in many packages amongst which Ardour and Audacity. There is also an example utility SoundStretch for audio file conversion (pitch, timebase and playback rate). Source code and binaries, together with a comprehensive article on time/pitch shifting basics, are on http://www.surina.net/soundtouch/index.html. I have built SoundTouch into a Pure Data external [soundtouch~].

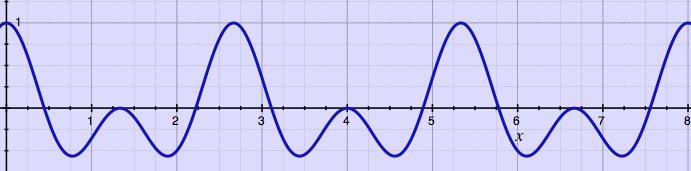
Compare the test plot below with the equivalent test from [tempophon~] above. The waveform similarity based method is a great improvement on the elementary rotating tape head emulator.

With harmonic sounds, the SoundTouch routines can find spots of best match for overlapping. With inharmonic combinations, this is virtually impossible because the waveform shows no repetition, at least not within the short time frame where SoundTouch must find it. This is not a defect of SoundTouch, but an inherent aspect of time domain pitch shifting. Therefore, the method does not work equally well for any arbitrary sound material. It works best for speech, monophonic instruments, and music with simple harmonic ratios or low complexity. Being a time domain method, SoundTouch shows some other side effects of cutting / inserting signal fragments: with downward pitch shifting, short attacks can easily get lost, while upward pitch shifting can induce audible repetition. With modest transposition rates, these effects are of course less prominent than with extreme settings.

The SoundTouch library is well commented and user-friendly. The code is efficient: realtime pitch shifting with SoundTouch is responsible for only 1% CPU time on my 2 GHz MacBook. Building a C++ library into Pure Data, which is pure C, is however not completely straightforward. This topic is described on the next page, [soundtouch~] for Pure Data.

frequency domain method

In frequency domain, a completely different handling of phase inconsistencies is possible. From Stephan Bernsee's comprehensive explanation on www.dspdimension.com, I learned how to do pitch shifting in frequency domain. It is quite abstract matter, and I always need a lot of illustrations to get hold on the elusive sinusoids. Let me illustrate the actual problem once more with a graphical example. Here, the overlapping segments of a stretched sinusoid are not windowed, to clearly show a phase shift:

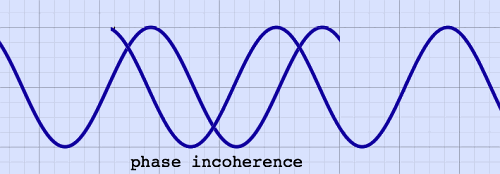Can we not just force the phases of successive signal segments to neatly coincide? This would be possible when all frequency components are isolated. A time shift has different phase shift effect for each frequency, therefore they must be treated separately. With all frequencies isolated, their phases could be registered, and the phase in the actual frame be synchronized with the preceding frame.

Isolating frequency components and shifting their phases, means to analyse, break up,and resynthesize the signal. To do that, we need to go to 'frequency domain', by applying Fast Fourier Transform, FFT. Lots of illustrations on this topic can be found in the FFT section, starting with the page Fourier Matrix. Complex numbers are also part of this story, and they are introduced on the page Trip to the Complex Plane.

Superficially, it could seem that pitch transposition in frequency domain is quite simple: just tranfer the FFT bin contents to other bins, depending on the pitch factor. Like shrinking or expanding the spectrum:

very crude representation of transposed frequencies

This view is not complete nonsense, but in practice, things are complicated. Be prepared for loads of details. A spectrum does not hold frequencies! It holds complex numbers, which can be mapped to other complex numbers, telling amplitude and phase of the initial complex numbers. The FFT bin numbers represent harmonic frequencies wich served as correlation functions to calculate the spectrum. For realistic FFT sizes, these bin harmonics are some ten, twenty, or fourty Hz apart from each other. So how do we get informed about precise frequencies?

If you would plot real and imaginary coefficients of one FFT bin for successive frames, you would see a kind of clock. When a steady sinusoid is correlated by that bin, the clock ticks at a regular speed. For successive, non-overlapping FFT-frames, a non-zero speed indicates by definition a frequency correlation which deviates from the FFT bin center frequency. Here is a visual impression on the complex plane:

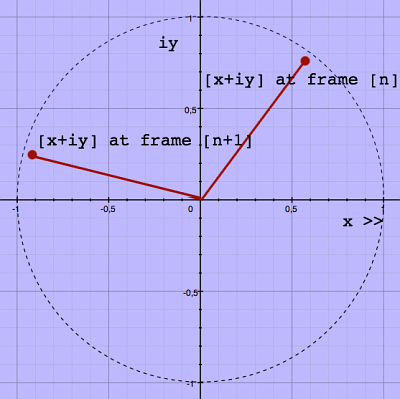If the above stated sounds rather vague, it is because I am trying to express things carefully. Frequency domain information is not that straightforward. Framewise Discrete Fourier Transform brings spectral leakage, and the correlation of one single input frequency is spreaded to some extent over all FFT bins. Therefore, the data should be interpreted with reserve. Here is a (full complex) spectrum illustration, copied from the page FFT Output, showing an example of spectral leakage from one single input sinusoid:

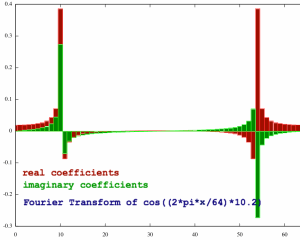The plot has a lot of coefficients, suggesting the presence of frequencies which were not actually there. Still they are all representatives of the input signal, in a way. Now imagine we employ the clock phenomenon, the phase increments, as an indicator of input frequency. This would give a lot of different answers.

To reduce ambiguity, an increased FFT frame overlap is recommended, with 4 times overlap as a minimum. Why does that help? Let me try if I can put that to words, and pictures. The clockwise or anti-clockwise rotation of the spectrum coefficients in their first appearance as [x+iy] coordinates give them room to express a phase-shift inbetween +/- pi radian, being +/- half a cycle. To the earlier example, I have added a green pair of points, showing a clockwise rotation which is by convention called negative:

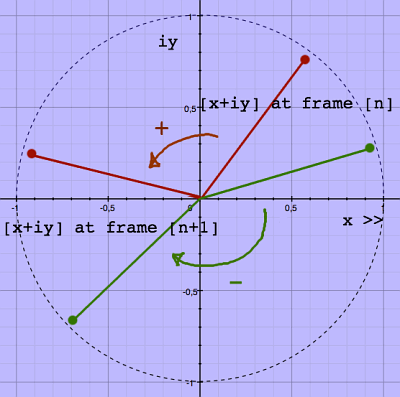This +/- half cycle room must be interpreted respective to the shift of the FFT bin center frequency over successive FFT frames. With no frame overlap, the bin center frequencies themselves will shift by multiples of a full cycle. The 'phase clock' can express a deviation within the bin, below or above the bin center frequency, and it has a total range of one cycle as well. For example, if the clock in bin nr 10 shifted half a cycle in positive direction, this indicates a frequency of 10.5, expressed in unit bins or FFT frame harmonics. Because of the spectral leakage, many coefficients have too little room to express the input frequency, as they can only express what fits in their particular bin.

shift range with no overlap

With four times FFT frame overlap, the bin center frequencies will shift multiples of only a quarter-cycle, respective to the input signal. Here is an impression in time domain:

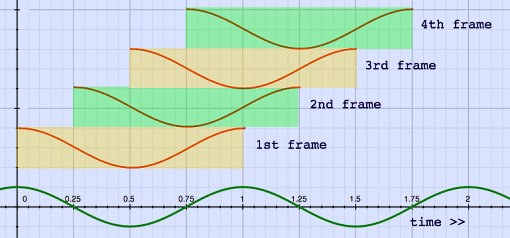FFT with four times overlap

But the coefficients still have the +/- half cycle range at their disposal, and they can now express a shift up to four times the bin center frequency shift. This means that they can express frequencies which belong in other bins!

shift range with four times overlap

The corrected phase shift (in cycles) and with overlap = 4 is now expressed this way:

step 1: phase-shift (in cycles) - (bin nr / 4)
step 2: wrap result in the +/- 0.5 cycle interval
step 3: multiply by 4

And the frequency, expressed in the form of FFT harmonics or unit bins, is this sum:

If a frequency is computed this way, it can be simply multiplied by the pitch shift factor to find the new frequency. This new frequency has to be transferred to the appropriate FFT bin, together with it's amplitude information. To find the new bin, the original bin nr is also multiplied by the pitch shift factor. Bin numbers can only be integers, and must be rounded in the direction of zero.

When the pitch-transposed frequency is in it's new bin, all the correction steps should be undone, now with the new bin harmonic number as a reference. This would mean:

step 1: subtract the bin harmonic number
step 2: divide by overlap
step 3: add the bin center frequency's phase shift
step 4: wrap into the +/- 0.5 bin interval

By the way, there happens to be a lot of mathematical redundancy in these steps. Never mind. The result expresses a phase shift again, still expressed in unit bins. Now comes the crucial step. The original phase shifts were actually result of phase differentiation. Now, to build the new spectrum, the transposed shifts or differences must be integrated with the transposed shifts of the preceding frame. Recall what happens with differentiation: the constant is lost. In this case, the constant was the absolute phase position, and it is lost. That was exactly the intention.

The integrated transposed phases, together with the amplitude information, can be converted to real and imaginary parts in the regular fashion with cosine and sine functions (which want phases expressed in radians of course). And then finally, back to time domain with inverse FFT.

This was a long journey to get the phases neatly glued together, and I have even omitted some practical details. The method is CPU-intensive, not so much because of the FFT's, which are efficient enough, but because of the trigonometric functions atan2, sin and cos. There is also an option to do the actual transposition in time domain, with fractional reading speed like in the rotating tape head recorder, and do the phase integration in frequency domain. This approach is described for Max/Msp by Richard Dudas and Cort Lippe on http://cycling74.com/2006/11/02/the-phase-vocoder-–-part-i/.

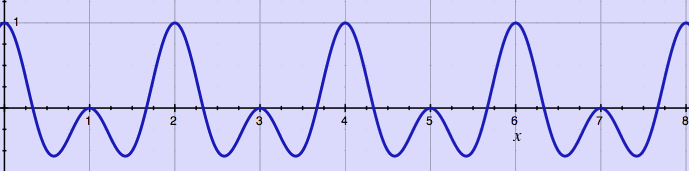
More than about CPU-load, I am concerned about the result. I have built the frequency domain pitch shifter into a Pure Data object [pitchshift~], so why not repeat the harmonic cosines test? The plots below show no amplitude modulation, and this holds for most frequencies. Instead, another unwelcome 'feature' has appeared: some frequencies are almost killed.

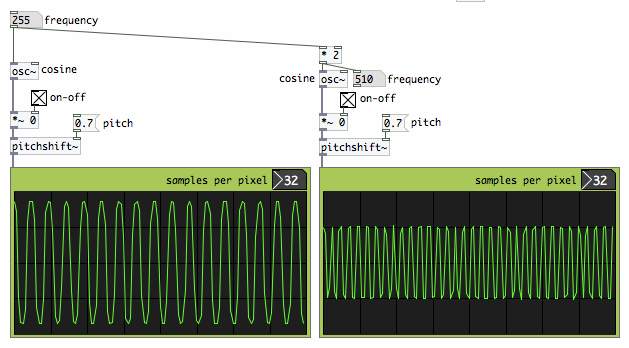Does it indicate some bug in my code? I do not think so. The amplitude differences are a notorious side-effect of elementary frequency-domain pitch shifting. What is the cause of it?

When starting up the pitch shifter, the phase integrator buffer is initialized with zero's for all bins. After all, there is no information yet at that moment, no preceding frame. If there is no significant input signal, there may be some noise, and the phase integrator buffer content gets randomized. When I start sending the test cosine in, the integrated phase differences make a reasonably neat pitch-shifted cosine output. But the phases have inherited the randomness of the preceding noise. The bins that should together reproduce the full cosine, may now partly phase-cancel each other! Look how orderly a cosine's phase spectrum normally is. We can not randomize this with impunity:

With the phase-diffentiator-integrator model, the output sounds inherit their absolute phase positions from their predecessors, not from the sound source. Therefore, it is not predictable what amplitude effects a frequency will suffer. This is illustrated by the patch below, where one cosine test signal is used, and the only difference is the moment when I start to send the signal to the pitch shifter. The output amplitude is different at every restart.

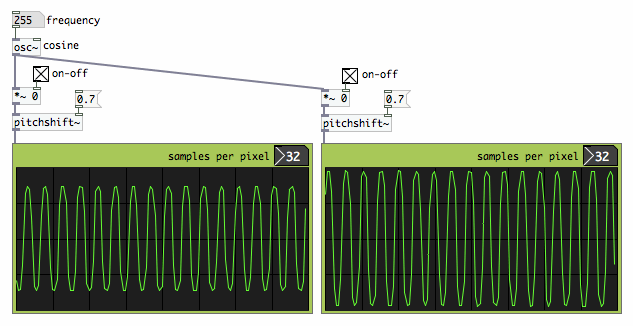The randomisation of absolute phase, and resulting amplitude effects, induce the sound character of comb filtering. Nothing can be done about this with simple means. In fact, what we want is to start a pitch-shifted sound with absolute phases, and then continue it with relative phases. Finding start-points, and keeping together all the bins that correlate one sound source, is really complicated stuff. For the moment, it is too difficult and time-consuming for me to explore. But at least, doing all these illustrations gave me a better understanding of the issues. It all boils down to the fact that FFT can not resolve single frequencies without spectral leakage.

Some detailed articles presenting frequency domain solutions are published. There is a comprehensible text by Axel Roebel on http://www.mp3-tech.org/programmer/docs/dafx32.pdf. An open source library for frequency domain pitch shifting with phase-resynchronisation is available from rubberbandaudio.com.

A different approach is developed by Stephan Bernsee in his work for Prosoniq and his own Dirac library. From minuscule snippets of information, I gather that these methods operate in time/frequency domain, employing complex-valued wavelets. It would be fascinating to learn more about that. Unfortunately, these inventions are too precious to be shared in the public domain. The same holds for the widely praised Elastique technology from zplane. These are closed source libraries which you can get (Dirac LE) or buy, not learn from.

conclusion

By definition, it is mathematically impossible to perfectly isolate frequencies within a real-world signal. Therefore, perfect pitch shifting seems to be a mission impossible, no less than building a perpetuum mobile. A simple, brilliant solution will probably not be found. Instead, advanced methods focus on many details of analysis in order to approximate the ideal result. All together, good quality pitch shifting techniques go far beyond the dsp hobbyist level. Considering these circumstances, it is fortunate that at least a few people have published the source code of their time stretch / pitch shift routines, so we can build it into applications of choice. The next page describes how Olli Parviainen's SoundTouch library can be built into the real time dsp environment Pure Data.