Complex Roots of Unity

This title sounds rather devote, but it concerns nothing more than computing complex roots of the number 1. The roots of unity pop up in the context of Discrete Fourier Transform. Once you know what they are, they simplify the concept of DFT.

Let us start from the assumption that root extracting is the inverse process of computing a power. The square root of 1 is 1 because 1*1=1. But -1*-1 is 1 as well, so -1 is also a square root of 1. There are two square roots of 1. If we take the cube root of 1, then -1 is not a solution because -1*-1*-1=-1. So the cube root of 1 has only one solution amongst the real numbers. But now let complex numbers enter the scene. On the complex plane, there exist three unique points of which the cube is 1. I have plotted these:

How does that work? First we have to recognise that e^(i2pi) equals e⁰, because the complex exponentials are periodic modulo 2pi. Further, e⁰ equals 1. Let us then compute the cube of the first cube root of 1:

The other complex cube root of 1 is (e^i2pi/3)², and the cube of that will give e^i4pi, which equals 1 again. The third point (e^i2pi/3)³ is on the positive real axis. It is our familiar number 1 of which the cube is also 1.

The integer complex roots of unity seem to divide the unit circle in equal intervals. How come? As we have seen earlier, the logarithms of complex exponentials on the unit circle are angles on the iy-axis. And root-extracting of a number is equivalent to division of it's logarithm.

Let us take a look at the three points again. All cube roots of 1 can also be defined as powers of the negative interval e^-i2pi/3:

But obviously, the points can not all be defined as powers of e^i2pi, because these powers will never be something else than 1.

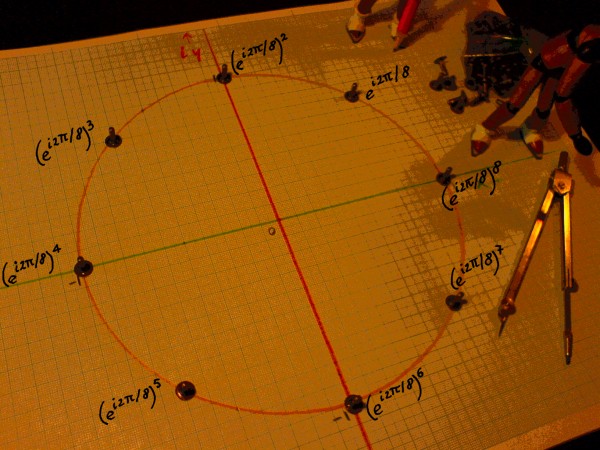
In order to further illustrate the pattern of roots of unity, I turn to a next example: the 8^th roots of unity. All points are depicted here as positive powers of the first interval, being e^i2pi/8. That interval can be denoted the primitive 8^th root of unity.

All points can also be described as negative powers of the primitive 8^th root of unity.

Complex exponentials have infinitely many aliases because of their periodic character. Aliases can be a nuisance, but sometimes they can be exploited to reduce the amount of computations. Anyway it is a good thing to identify aliases. If we use n for the n^th root and k for the k^th power, both being positive non-zero integers, the following identity holds:

Here is an example that can be checked with the preceding illustrations.

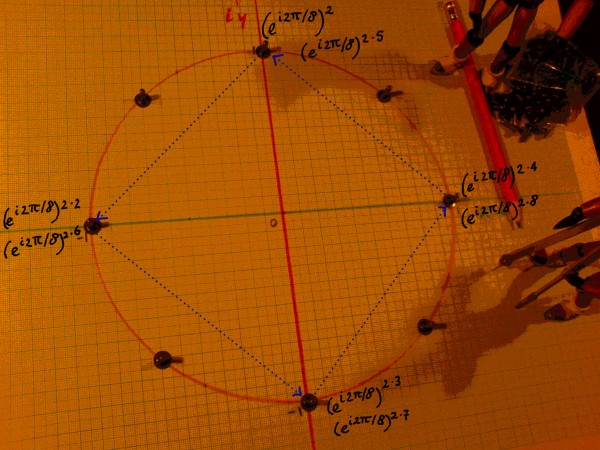
Below, the  powers of (e^i2pi/8)² are illustrated. 4 unique points on the complex plane are visited twice. Therefore, these points can also be described as 4^th roots of unity. Instead of (e^i2pi/8)², write (e^i2pi/4). Because (e^i2pi/4) is the square of (e^i2pi/8), it must be the case that (e^i2pi/8) is the square root of (e^i2pi/4).

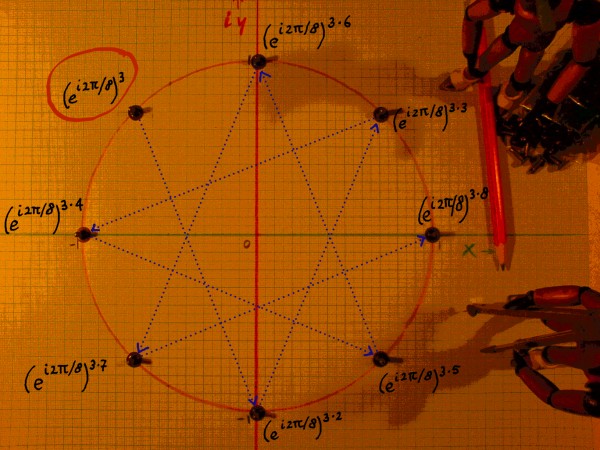
And down here, the powers of (e^i2pi/8)³ are illustrated. It ends in 1 again, proving itself to be an 8^th root of unity. These powers happen to alias all powers of the primitive root e^i2pi/8, but they appear in a different order.

The successive powers of an n^th root of unity describe discrete points of a complex sinusoidal function. A convention, or maybe a just a lazy habitude, is to specify such a series by naming the first interval of it. Let me plot the sinusoids of e^i2pi/8 in the real plane:

And here is the series of the next root, (e^i2pi/8)²:

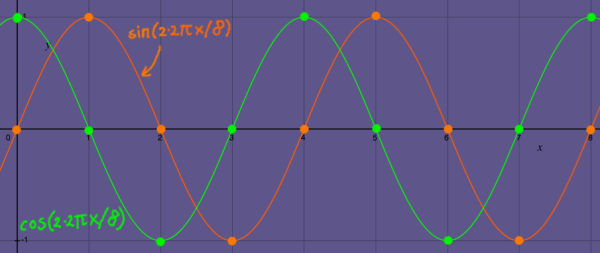Now let me try some trick with the roots of unity. Because (e^i2pi/8)*(e^i2pi/8)²=(e^i2pi/8)³, it should be possible to compute the next complex pair of sinusoids from the two preceding pairs:

(cos(2pix/8)+isin(2pix/8)*(cos(2*2pix/8)+isin(2*2pix/8)
=(cos(3*2pix/8)+isin(3*2pix/8)

My plotter gives the real output, that is the cosine, of 3*2pix/8 indeed. It does not output imaginary numbers on the real plane of course, therefore the sine part in the plot is computed separately to complete the picture.

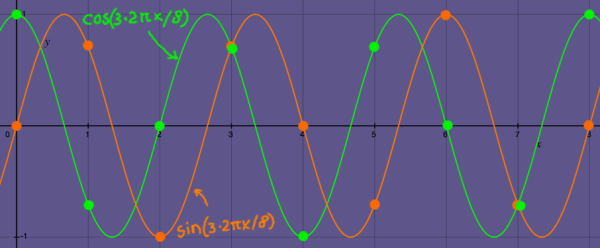In fact, all 8^th roots of unity, apart from the primitive root, can be computed as a product of two others. Of course, a similar rule holds for other n^th roots.

We can use this to our advantage. We multiplied the powers of the primitive 8^th root with those of the primitive 4^th root and obtained a third series. They are pictured below. But when we take the square root of the 8^th root, we can go one step further, that is, to the 16^th root.

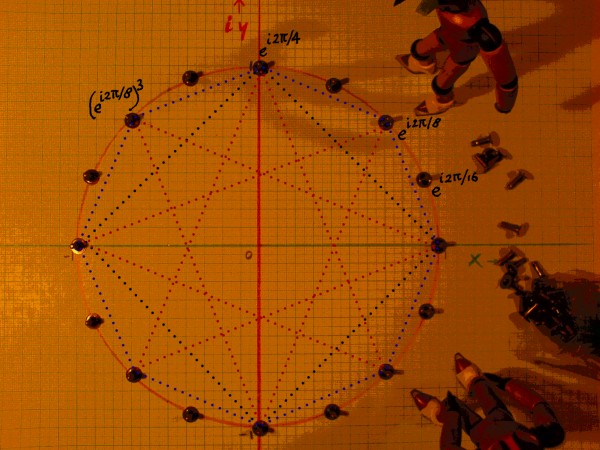I multiply the three series that we had until now, with the series of the 16^th primitive root. From this multiplication three new frequencies result. Together with the old frequencies and the 16^th primitive root, this gives already seven different frequencies.

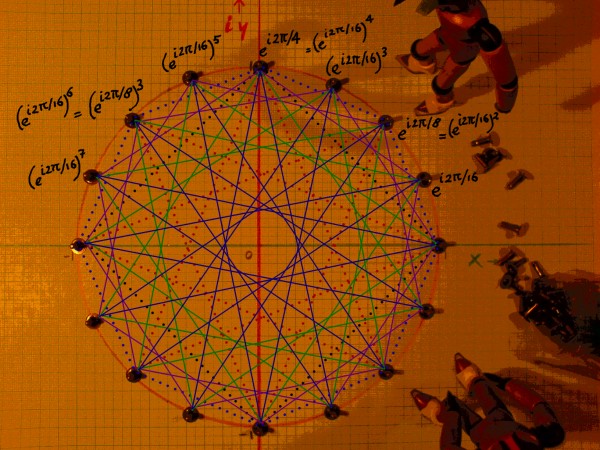Continuing this pattern and multiply with the 32^th primitive root, would fill the spaces between the existing frequencies again, resulting in a total of fifteen frequencies. Drawing that would be a mess, so I decided to do another type of illustration. I made a MaxMsp patch that can do these multiplications. It has a cascade of five complex oscillators, going down till the 64^th root of unity, and four multiply-and-add procedures.

Audacity's spectrum analyzer tells this about the outputs: 31 evenly spaced frequencies, the first being around 690 Hz and the last one around 21360 Hz.

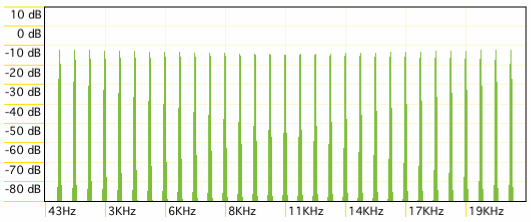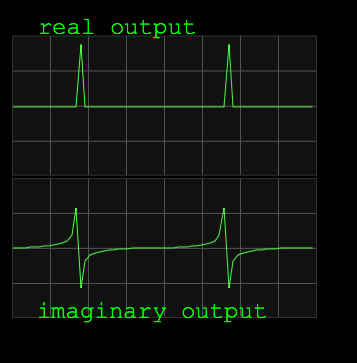
Real output and imaginary output have the same spectrum, but their waveshapes differ. These shapes are remarkable anyway. They are both approaching a pulse. That is no coincidence. A pure pulse contains all frequencies (in phase), and here we are on the way to that state. My page Quadrature Mixing has more detailed plots of multiplied complex sinusoids.

It was only a few minutes work to expand the MaxMsp patch with three more oscillators: the 128th, 256th and 512th root of unity. Now we have 255 evenly spaced frequencies, starting at 86 Hz.

My eight complex oscillators are at 86.13, 172.26, 344.53, 689.06, 1378.16, 2756.25, 5512.5 and 11025 Hz. These are octaves. The generated frequencies are all harmonics from 86.13 Hz to 21964 Hz, 255 harmonics in total. Not one single harmonic is missing.

The reason for doing this experiment was not because of the beautiful sound. Hah! You would not want to hear it more than one time. No, I was driven by curiosity. Roots of unity, and roots of roots of unity, and roots thereof etcetera, are an essential ingredient of Fast Fourier Transform. I just wanted to play around with it, because it is quite abstract otherwise.