Resampling with Chirp Z

Since chirp Z transform can zoom in on a specific segment of a signal's spectrum, I would think it can be used for downsampling or upsampling purposes. That is indeed the case. I did not now what to expect precisely, so I figured out by experiment how to do it.

Below is a test function consisting of two cosines with periodicity 1 and 3 in an FFT framesize of 1024 samples.

I zoom in on the spectrum with zoomfactor 2. As ever, this spectrum looks inconspicuous:

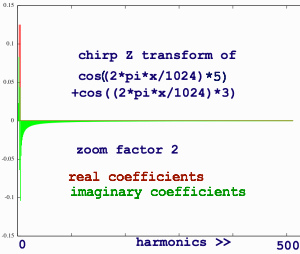I feed this spectrum in a regular inverse FFT. What comes out, is the signal downsampled by a factor 2:

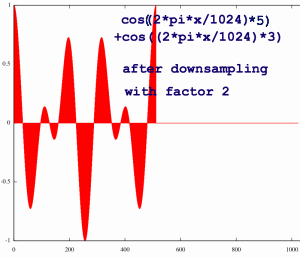So by zooming in on the spectrum, which is in fact upsampling, the signal can be downsampled. That is funny. Of course, this downsampling was not such a difficult task. It could be done by taking away every other sample, instead of the chirp Z transform with it's two complex FFT's of double size, plus a regular inverse FFT. Therefore, I will try a weird downsampling factor like 1.5:

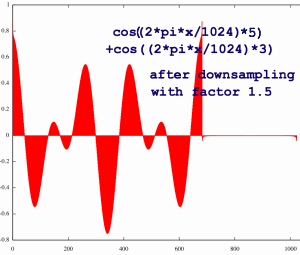Such downsampling can also be done by 'fractional resampling', where you first upsample and then downsample, the factors being a ratio of relatively prime integers. That would require a lot of filtering. But, can chirp Z downsample without filtering? To check this, I add a frequency in the second half band, at harmonic 280 (Nyquist is at 512). This is my test signal:

Doing chirp Z transform with zoom factor 2.2, for example, the upsampled spectrum has a peak above the Nyquist frequency, originating from harmonic 280. That peak has no conjugate. In fact, after stretching the spectrum, nothing has a conjugate anymore.

Reverting this spectrum back to time domain, would give the signal plotted below. The high frequency comes from the peak above Nyquist. It can not be harmonic 280 since the downsampled signal has harmonics up till around 230 in the positive range. It is an alias of a frequency that was not in the original, and should be eliminited.

The solution seems simple. When we are in frequency domain anyway, a mirrorsymmetric spectrum can be computed from the first half, to get rid of aliases. The result is a bandlimited & downsampled signal:

Chirp Z can downsample with any factor, integer or not. On the previous page I zoomed in on a 1024 point spectrum with factor 200. An inverse FFT of that would give a 5 point signal, pretty useless I would think. Here is my test signal downsampled with factor 8, to have another impression:

As the signal gets sleeker, the sample value peaks grow. Apparently, the increase is proportional to the zoomafactor so this can be compensated in the normalisation. Also notice that the 'empty' range is not really empty, it even starts with a dreadful peak. A similar peak appears at the start of the downsampled signal, although it is hard to see in the plot. Let me do a magnified plot of the first 75 samples. It turns out that the signal extremes are not so perfectly interpolated at all. The distortion is probably caused by the mirrorsymmetric spectrum computation. Relevant information about the waveshape was in the second spectrum half, which is erased by that action.

I wanted to try signal upsampling as well. With that I had such weird results, until I realised the input signal should leave room for expansion. Just like the downsampled signal shrinked and thereby made room. So here is my input test signal again, but at half the length of the analysis:

I feed it into the chirp Z transform with zoom factor 0.8. That is zooming out instead of zooming in. What happens when zooming out? The opposite of zooming in. It is hard to imagine what that means. Only after experimenting, I could understand the effect. You are not seeing a segment of the spectrum, but the whole of it and even a bit more. While the spectrum shrinks, point N (1024) which is also point zero because of the periodical nature of the transform, moves leftward. In the plot below you can see how the coefficients in the lowest part of the spectrum are thereby copied to the right of this shifted N aka zero point.

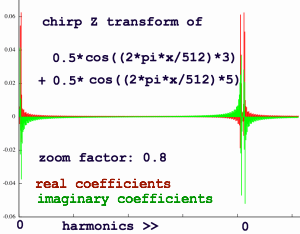Just like with zooming in, the spectrum is not mirrorsymmetric anymore. Reverting this to time domain as is, will give the signal plotted below. The upsample factor is the reciprocal of the spectrum-zoom-factor:

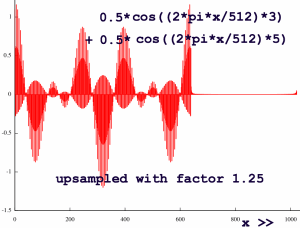The high frequencies here are what they call 'image' frequencies, because they are kind of ghost image from the lower spectrum part. Images will always appear in an umsampled signal, no matter how bandlimited that signal was. With chirp Z we can get rid of the images by computing a mirrorsymmetric spectrum from it's first half, exactly like it was done for downsampled signals. Now I get this nicely stretched output:

Upsampling with chirp Z brings an extra problem that must be handled. So far, I did low frequencies and it worked well. But with high frequency content in the original, we will be bothered by conjugates. After all, with point N shifting leftward, the conjugates also shift leftward. Let me enter a high frequency to check what will happen. First do a non-zooming transform to see the original spectrum:

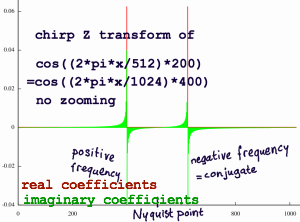If I zoom out using factor 0.75, the negative frequency correlations already tresspass the middle of the analysis frame in their leftward movement:

We have to perform bandlimiting to eliminate such tresspassers. The Nyquist frequency must be tracked in it's movement. It moves like:

shiftedNyquist = Nyquist * zoomfactor

Everything between shifted Nyquist and original Nyquist must be zeroed, before computing the mirrorsymmetric spectrum.

To visually check if this works, I have to upsample the signal drastically with factor 100. Otherwise we will only see those indefinite needle bunches. On the left is the non-bandlimited output. It is diluted with zero's, which means it has alias frequencies. On the right is the bandlimited output, it has the pure transposed frequency.

This extreme upsampling was done for testing purposes, but it would not have worked if there had been frequency content below harmonic 100 of the analysis width. Such content would wrap around in the limited space. There is however also this option to rotate the whole spectrum with a frequency offset. If we make the bandlimiting function dependent on the frequency offset as well, the options for resampling increase further. Although the offset is effectuated by complex multiplication, the offset itself is not a factor but a frequency addition. To find the frequency cut off point:

shiftedNyquist = (Nyquist-frequencyoffset) * zoomfactor

Using this modification, I have checked that exactly the same result as in the above experiment can be obtained with a frequency offset of harmonic 392 (harmonic respective to analysis width) and zoom factor 0.5. But now without worries about possible distortion by low frequencies. In serious applications, this bandlimiting should probably be done with some very short curve instead of hard cut.

In this quick test of chirp Z as resampling method, I have not touched on all possibilities. But so far, I am impressed. The method is computationally intensive, on the other hand it is very flexible. Spectrum rotation for example, is 'included in the price'. You can magnify any aspect of a signal by a combination of rotation, zooming and filtering in one single process.