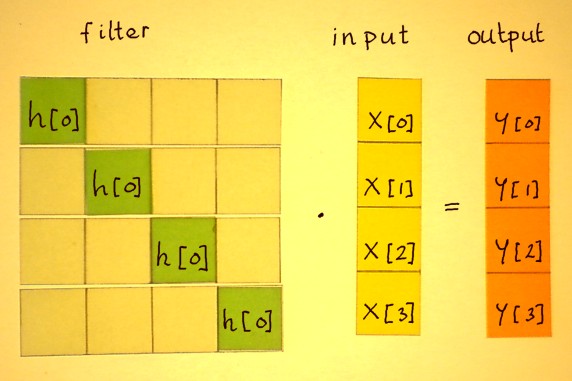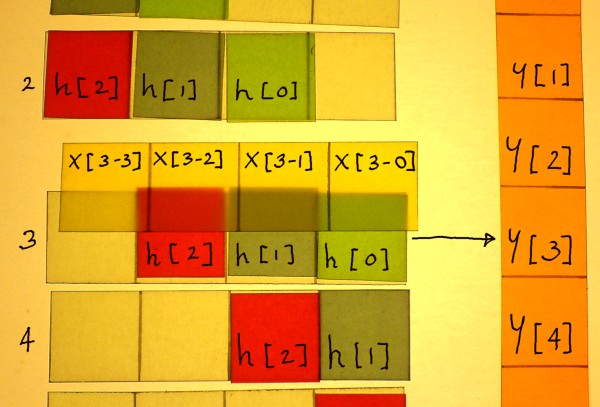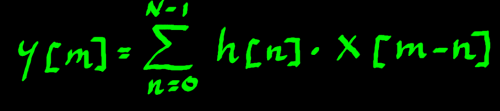A Matrix Operation
|
Convolution can do (no more than) amplification and attenuation of frequencies by means of phase cancellation/reinforcement. The popular name is therefore: filtering. |
 |
In convolution, three arrays of sample values appear:
an input array x[n]
an impuls response array h[n] (the 'filter')
an output array y[n]
[n] denotes a sample index number. The index can be related to time or space if you want. The impuls response h[n] is responsible for the amplification / attenuation. For convenience I will call that array 'filter'. Only later on this page I can illustrate what it means that the filter is an impulse response.
Below is the simplest of convolutions as an example to start with. A
one-sample 'filter' h[0] is on the main diagonal, which is also called
identity diagonal. The input array and output array are vectors of
equal length here. They could be streams of audio with a million or a
billion of samples as well. That would make a very big square filter
matrix, but still with only one diagonal.
 |
Such a convolution with h[0] can only amplify or atttenuate all
frequencies at the same time. Not what we call a filter yet.
Let us next do an example with a two-sample h[n]. That can already make a useful filter in practice. If you inspect the rows of the filter below, you will notice that the array h[n] appears time-reversed in the matrix. That is a major aspect of convolution.
As compared to the one-sample filter, an extra row in the filter matrix, and thus in the output, is required to complete the convolution with the two-sample filter.
 |
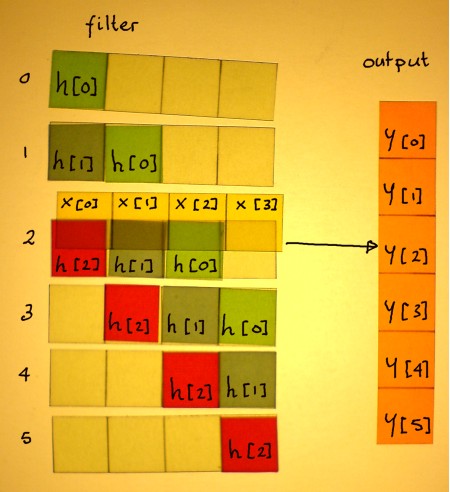
One more example to see the system of it. The diagonals are
constant. All filter coefficients
h[n] have a fair share in the operation. They appear as many times as
there are input samples. There is also a rule of thumb for the output
array-length:
N[filter] + N[input] -1 = N[output]
In the example below it is: ((3+4)-1) = 6
 |
Below, the correlation for output index y[2] is illustrated as an
example. The rows of the filter matrix are numbered, and they
correspond to the output rows. Notice that x[2] is multiplied with the
filter's identity diagonal. Furthermore, some older samples of x[n] are
used.
 |
Fortunately webpixels cost nothing so I can afford doing lots of
pictures. Below is the correlation for y[3]. It is almost hard to
distinguish it from the preceding picture, because the operation is so
systematic. So let us try to identify the pattern of it.
 |
Admittedly it took me quite some time to disclose the pattern in a
sensible way. But look, the index number of x[n] can be described in
terms of the y[n] and h[n] indices.
 |
In order to write the whole thing in an algebraic formula, some
index letters will have to be renamed, unfortunately. I suggest that we
use x[m], y[m] and h[n]. Then the whole convolution can be described
efficiently in terms of the arrays:
 |
In words: y[m] = the sum of all products h[n]*x[m-n].
Suppose the filter array is a fixed buffer and the input array is a
stream. Then it would be effective to keep older values of x[n] in a
circular buffer or (multitap) delayline. That is indeed how filters of
modest length are done. Below is the flowchart of the example filter.
 |
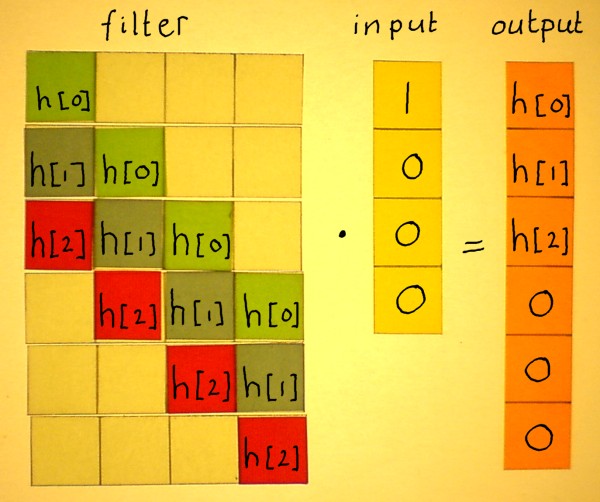
One question is still not answered: why is h[n] called 'impulse
response'? Again, this can be illustrated nicely with a simple matrix
(I love them). For the input array x[n], we choose a unit puls or
impulse as it is called. In the digital domain that means: a
samplevalue
of 1 on x[0] and zero's everywhere else. Now look at the output (the
response to the impulse). It is the filter array itself! So at the
ouput
it appears in the normal time-direction....
 |
The filter matrix implements reflections. The later reflections
(higher index numbers of h[n]) have a longer delay time. That is why
h[n] appears time-reversed in the matrix operation. The higher h[n]
indices must operate on older samples of x[n]. And older samples means:
lower index numbers.
There is a strong analogy with acoustic reflections. Imagine you do
a pulse in a reflective space, by clapping your hands once. The
response to that pulse is: the direct sound h[0], the first reflection
from a nearby surface h[1], and the second reflection from a surface
further away h[2]. These reflections will also do phase cancellation
and reinforcement, thus filtering.
 |
The impulse response is a soundwise blueprint of a space or system.
Once you have captured it digitally, or computed an idealised impulse
response, you have your filter array.