Phase Decomposition

Sometimes you need to split a signal in two or more phases and keep (one of) these in seperate shorter arrays. That process is equivalent to downsampling. From a matrix perspective, it can be considered a row permutation. I want to illustrate phase decomposition as a matrix operation here.

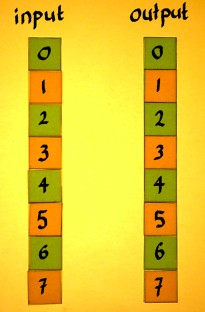
I will start from the identity matrix, and later convert that to a downsampling matrix. The input vector is a series from 0 to 7, so we can track where they go. Multiplication with the identity matrix, of course, gives an output identical to the input.

We can remove the entries from the odd rows in the identity matrix. This is not yet a downsampling matrix. It only removes the odd phase from the signal.

The empty rows themselves have to be removed as well. Now there are four rows instead of eight, and also four output rows. There is a 'double shift' in the rows: the identities do not move rightward one cell, but two cells at a time.

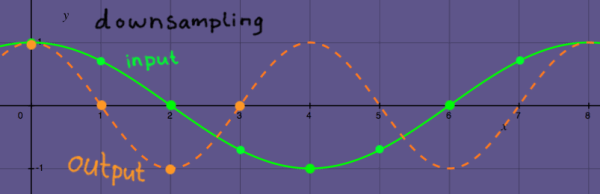
Of course it is also interesting to check what downsampling does to a waveshape. I plotted a simple 8-point cosine to illustrate that. Downsampling basically doubles the frequency, in contrast to the suggestion of the word.

However, double frequencies can not always be represented. When they go over the Nyquist frequency, we get the alias. In the case below, I started with the Nyquist frequency as the input. The output vector represents DC.

Two such rectangular downsample matrices can be combined. They split the input vector in two phase vectors of length N/2. This is even-odd phase decomposition. It is an ingredient of radix 2 Fast Fourier Transform. And because I want to know how FFT works, I am exploring phase decomposition here.

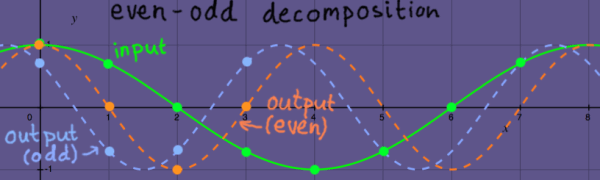
Below is a plot of a cosine example, now downsampled into an even and odd vector. Notice that the odd output represents the same doubled frequency, but with a phase shift. That originates from the one-sample shift of the odd phase in the original frequency.

The two N/2 vectors can be further decomposed. The NxN matrix must then contain two square N/2xN/2 matrices with two rectangular downsample matrices each. Although the matrix looks different, the underlying process is the same: downsampling by a factor 2.

After downsampling the eight-point vector two times with factor 2, we now have four two-point vectors. Theoretically, these can be downsampled one more time, in order to get one-point vectors. Although the operation is trivial, I have done the illustrations of it, to complete the pattern. There is 8 small rectangular downsample matrices here. But it looks and works exactly like the identity matrix. That's funny eh.

By the time all stages of phase decomposition are done, most frequencies will have been pushed over the Nyquist edge in one direction or the other. For the Fast Fourier Transform, that does no harm. An FFT must be done with complex vectors and complex multiplication anyway. Any real input is converted to complex immediately. Then you have no aliases, but conjugates which keep all positive and negative frequencies neatly separated.

When we compare the binary values of input and output numbers, we see the famous bit-reversal which is typical for an N-point vector decomposed into one-point vectors. This is not coincidence, nor magic.

Sorting samples into 2 phases, is sorting to low and high bits actually. In the first stage, the even and odd input was sorted to the most significant output bit. In the second stage, to the second-most significant bit. This system would work for any N=2^x. Below, I indexed the row and column numbers in binary, to illustrate the idea without further comments.

Row permutations can also be utilised for upsampling. Start from an identity matrix again. Instead of deleting rows from the identity matrix, we now insert empty rows. Look what such an upsampling matrix does: an input vector is stretched to twice it's length. The empty places between the samples in the stretched vector are supposed to be filled with zero's.

We can combine upsample matrices to interleave two N/2 length vectors into one N length vector:

Or we can interleave four N=2 vectors into two N=4 vectors, like here:

But this matrix is, apart from my colours and dotted lines, exactly the same as the 2nd stage decomposition matrix earlier on this page. I will copy it for comparison:

What is happening? Are these processes the same? Not precisely, in general. It took me a while to perceive the pattern, but after all it is damn logical: the interleaving matrix is the transpose of the corresponding decomposition matrix. You can check that in the figure below. The rows of the decomposition matrix become columns in the interleaving matrix. And because there is always unit vectors in each row/column, it is exactly the inverse.

Downsampling, upsampling, phase decomposition and interleaving can also be done with factors other than two. If only N is an integer multiple of the factor.