Sparse Matrices

Sometimes a multiplication matrix can be decomposed into several factor matrices, reducing the amount of computations. Specially for large matrices, this can result in factors with very few entries, as compared to the original. Hence the word sparse. On this page I want to illustrate the notion of a sparse matrix in the most general way, using an example with only identities.

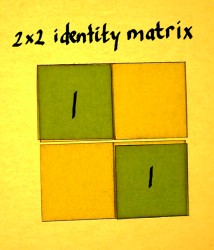
Below are three different NxN identity matrices. With the help of these, we are going to construct three sparse 8x8 factor matrices, the product of which will be a full 8x8 matrix with all entries filled.

I will combine multiples of these small identity matrices into the three 8x8 factor matrices. Here are four 4x4 identity matrices combined into one 8x8 matrix:

In a similar way, four 2x2 identity matrices are combined into one 4x4 matrix. And two of such 4x4 matrices are then put on the main diagonal of an 8x8 matrix:

This pattern should be continued with the 1x1 identity matrix. Four of them are combined into a 2x2 matrix. And of these, four copies can be put on the main diagonal of an 8x8 matrix.

We now have three 8x8 matrices, all made up of identity matrices at different resolutions. Each matrix has two entries per row. Whe will multiply these matrices one by one, starting at the right side, as is the convention.

When multiplying the first two matrices A and B, we could look at the output on a cell by cell basis, but that is not necessary. We know that a matrix, multiplied by an identity, is not altered. As matrix B has an identity in each quarter segment, it is easier to just inspect what they will do to the segments of A. In the first place, the entries of A will be preserved. But the identities in B will also make copies of A's filled quarters into the other quarter segments. The output matrix has a doubled amount of non-zero entries.

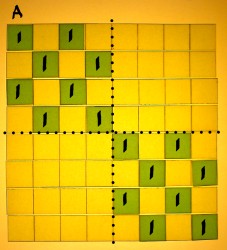In the next multiplication stage, the process is repeated. But now it is at a different resolution. A*B has identity blocks of size 2x2, copying the 2x2 blocks at the main diagonal of C to all other parts of the matrix.

So we had three sparse factors, producing a full 8x8 matrix. But how sparse are these factors actually? Imagine you want to process an 8 point input vector. That will cost two multiplications and one addition per row of each sparse matrix, so 16 multiplications and 8 additions per stage. That makes 48 multiplications and 24 additions in total, for the three stages. While multiplication of the vector with the full 8x8 matrix at once would cost 64 multiplications and almost as many additions.

Our savings were not so impressive yet. Designing an 8x8 matrix as 3 factors may not be worth the effort. But for larger N, decomposition becomes more economical. That is because the two-entries-per-row system can be continued. Below is an impression how you could expand to a 16*16 matrix.

For larger N, the factor matrices become more and more sparse. The pattern is: ²log(N)*2N entries in total for a likewise decomposed N*N matrix, as opposed to N² entries for the full matrix.