Bitwise & Poundfoolish

This pages shows matrix illustrations with indexes in binary numbers. Each bit in a binary integer represents a power of two which can be present or absent. This is how index values live in a computer. There is all kinds of bitwise operations and manipulations that you can do on integers. Such operations are elementary and fast. So you can save a nanosecond here and there. (After spending precious hours to find out how).

Although matrices for transform can theoretically have any number NxN, choosing a power of two for N tends to simplify implementations. Below, an 8x8 matrix is sketched with indexes in binary numbers. As indexing generally starts with 0, 7 is the highest value and only 3 bits are used to represent the indexes. The most significant bit points to the four quarters of the matrix:

The second-most significant bit points to squares at a finer level of resolution:

This pattern is continued till the finest resolution level.

I want to illustrate a frequently used example of bitwise manipulation. Say we multiply row indexes by column indexes like it is done to find the powers for W^kn of the Fourier matrix. Below is an example matrix for N=8. Only three bits are of concern. When we mask the more significant bits that are in a datatype, we see only the 'remainder' as it would show up after modulo N division. For example, binary 111*110=101010. The three least significant bits are: 010. And 7*6 modulo 8 is 2 indeed. Masking bits is a very easy operation, using a bitwise-and with N-1. Computing a modulo N division for N not being a power of two is much more complicated.

When working on radix 2 bit-reversal methods, I spotted the 'not-identity-diagonal', perpendicular to the identity diagonal. On this diagonal, the column index is the (masked) bit-wise negation of the row index. For N=2^x, a bit-wise negation of n is always N-1-n, and the not-I-diagonal divides the matrix in two triangular halves. The masked negation of n can also be found with an exclusive-or operation with the mask itself. The effect of exclusive-or with the mask N-1 is to flip the status of all bits. Example for N=8:

100   (binary 4)
111   (binary mask N-1=7)
---   (x or these values)
011   (result is binary 3)

The values 4 and 3 are additive complements within 7. In general, n and (n^N-1) are additive complements within N-1 for N being a power of 2. The ^ character is the C syntax for the exclusive-or operation.

Bit-wise-negated entries in a square N=2^x matrix appear systematically as pairs rotated over 180 degrees. Here is the not-I-diagonal, and an example of such a pair:

I am still in the process of discovering ways to employ bitwise negation. Examples are on the pages Bit Reversal and Inverse FFT.

It is sometimes useful to scan the status of a specific bit in an indexnumber n. This can be done by using a bitwise-and operation (bitmask). For the plot below, I scanned the six bits in indexes n from 0 to 63, by running over all n six times with a different mask:

n &= 1;
n &= 2;
n &= 4;
n &= 8;
n &= 16;
n &= 32;

I found that visualisations like this help me in finding solutions. When gazing at the above figure, I spotted a method for iterating over the odd blocks of specific resolution, without branching. For example, if I whish to iterate (incrementing) over the dark blue blocks in the above illustration and skip the inbetween values, I can simply add the following in C:

n |= 8;

The bit representing 8 or 2³ will always be set by the inclusive-or, so values without this bit set are excluded from the sequence. In a decrementing sequence this would result in an infinite loop.

An interesting sequence is formed by the isolated least significant set bits that are in a natural binary series. It is a series of pure powers of two. I have plotted their values:

A very simple routine exist, to extract this least significant set bit from a bit pattern. I have learnt this from topcoder.com, see http://www.topcoder.com/tc?module=Static&d1=tutorials&d2=bitManipulation.

The C code for this could be: extracted_value = n & ~(n-1);
Simple as it may be, I like to do an illustration of these operations.

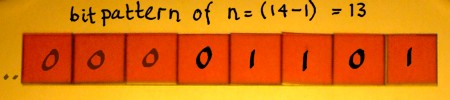Subtracting 1 from n clears the least significant set bit in n, and it sets all less significant bits high. In the example that happens with the least significant bit. Of n-1, all bits should be inverted with bitwise-not, which is written ~ in C. For the example, it is ~13.

And the next step:

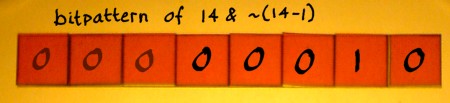~13 is 4294967282 when using a 32 bits unsigned integer datatype. It is also (232)-1-13. When 14 and ~13 are bitwise-anded, only one bit remains set. That is the least significant set bit in 14. It represents 21, being just 2.

It is also possible, and sometimes more convenient, to have the base 2 logarithms of the above sketched values. Such logarithms happen to coincide with the number of 'trailing zero's' that predece the first set bit. For example:

001000 is decimal 8 and has 3 trailing zero's
the base 2 log of 8 is 3

That pattern of trailing zero's in a natural series is plotted here:

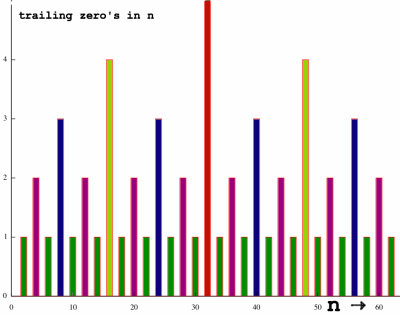Trailing zero's must be counted somehow. There is no  ANSI C operator for this. Some processors have an instruction for it. But counting zero's with a loop is also quite efficient. Odd numbers have no trailing zero's so you may skip counting that. How many trailing zero's are there in total, for a given series N=2^x? I think N-1 trailing zero's theoretically, but the zero's of zero must not be counted because these do not trail anything. Moreover, the zero's in zero would dramatically spoil the intention of your routine. Here is an example for N=8:

000   do not try to count the trailing zero's in zero!
001
010   1 trailing zero
011
100   2 trailing zero's
101
110   1 trailing zero
111

It is easier to count ones than zero's, therefore I negate the value of n bitwise before starting such a loop. The counting must continue while notn&1 (bitwise-and) is true. In C code:

There is more ways to implement this, I picked the following one from the page 'Bit Twiddling Hacks' by Sean Eron Anderson:

With the pattern of extracted powers of two, yet another interesting pattern can be created: a so-called Gray code sequence. Start with an array-variable initialised at zero and toggle-switch the bits of it one by one, doing exclusive-or with the extracted powers of two. Iterating over n, this could be done with the snippet from Topcoder that I illustrated earlier:

If a Gray code sequence is plotted as output values, the pattern shows no clear symmetry. But I was quite surprised by the individual-bits-pattern of it:

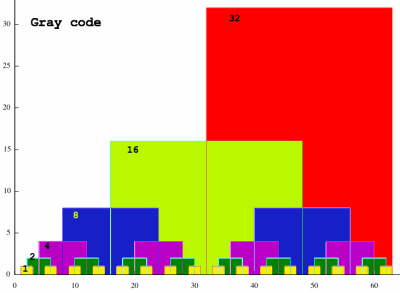Here is the natural sequence once more, for reference:

So far I have plotted quite some bit patterns, but what is the use of it all? To be honest, I don't know. That is, I am still in the process of exploring. You can find applications for the above mentioned patterns on my FFT pages. That is all I have at the moment. I documented the plots and codebits so I can stare at them every now and than. Soon as I have more, this page will be updated.