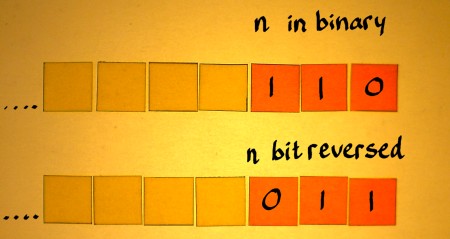Bit Reversal and Permutation

for Radix 2

In order to use the FFT schemes of the preceding pages, I need a method for bitreversed permutation of the output arrays. Although bitreversal is generally considered a rather trivial aspect, I find it more complicated than the FFT proper. In every FFT stage, the array entries are intertwined in a systematical way, the pattern of which is quite clear. But in the decimated end result, things appear shuffled beyond comprehension. To unravel, you would not want to spend so many iterations as in the whole FFT, like the naivest bit-reversed permutation methods do. More efficient methods tend to be rather enigmatic however.

On this page I want to develop a visual sense of bit-patterns and ways to manipulate these. I will start from scratch. First find a routine to reverse the bitpattern of one integer. Then figure out a way of swapping the relevant components within an array of length 2ⁿ.

Here is an example of a bit-reverse ordered output array like it could result from an FFT routine. The figure is copied from the page Phase Decomposition, where I illustrated how repeated downsampling shuffles the entries in an array. It needs reorganisation before it makes sense as being harmonics within a spectrum. Let us take one example pair of entries that must be swapped. Harmonic number 6 is at the location where 3 should be, and 3 is where 6 belongs.

Below I have expanded both entries as binary numbers. So we are looking at individual bits now. An integer datatype can have 32 bits for example, but here we would need only three of these.

General-purpose CPU's have no bit-reversal instruction, as far as I know. Anyway there is no ANSI C operator to addres such an instruction if it would exist. It would be so convenient if you could just write something like n ><= 3, to do the above sketched bit reversal. Instead, we have to write a loop to reverse the bits in one integer number. Let us do it then.

To start, we store a copy of n in a separate variable.

The bit-pattern of n must be shifted right one position, and it's least significant bit falls off.

At the same time, copy-of-n is shifted left by one position. The vacant positions in n and copy-of-n are filled with zero's.

It seems that the bit-reverse of n is already found. But that is coincidence. We must continue systematically till all is done.

We will now scan the least significant bit of the shifted n. That is the second-least significant bit of the original. The scanning can be done by a bitwise-and operation. The unsigned integer value 1 masks everything but the LSB.

This bit-of-n is then transferred to copy-of-n by inclusive bitwise-or. This works because copy-of-n always has a shifted-in zero at that position. It takes the true value when bit-of-n is one, or remains zero when the bit-of-n is zero.

The series of operations is repeated:
shift n one position right,
shift copy-of-n one position left,
give the LSB of n to copy-of-n.

After two iterations we have the LSB of the original three-bit n at the MSB position of our copy-of-n. The loop of operations should end here. But one thing remains to be done after that. The variable copy-of-n has now decimal value 27. A last bitwise-and operation is required to mask everything but the three least significant bits that we use. The mask has value 7, which is N-1. The result of this masking is that we finally have the bitpattern 011.

Notice that the count of iterations is one less than the count of bits used for the values, because the LSB of n is the most significant relevant bit in copy-of-n. Here we have the above sketched bit-reversal written as a C function:

This loop could perform redundant iterations. Imagine you have N=1024 which uses 10 bits, and do a bitreversal for n=3 which turns bit pattern 0000000011 into 1100000000. After one iteration you already have the set bits, but 8 more iterations will follow. From the page 'Bit Twiddling Hacks' by Sean Eron Anderson I learnt a modification to avoid that redundancy. The loop can end when the shifted n has become zero.

With this code, the loop will end as soon as all high bits of n are shifted out, and nrev receives a compensating shift after the loop end. Later I understood that this will save only one iteration on average. But never mind, we need a count variable of some sort anyway.

So far we have code to compute a bit-reversed version of only one integer. To visually check what happens to bitpatterns, I have plotted the indexes 0 till 63 with their bits separately shown. Here is the plot for n with the bits in their orignal order:

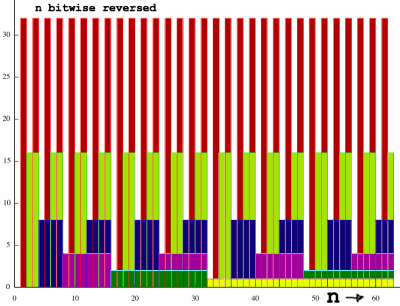
Below is a plot of the indexes with their bitpatterns reversed. For example:

at index 000001, 100000 is plotted with it's individual bits
at index 110110, 011011 is plotted with it's individual bits

All the bits representing decimal 1 are now regrouped in the second half of the plot. So all odd numbers are in that part. All bits representing 32 are now spread evenly over the range. Etcetera.

Now we are going to reorganise an array according to the bit-reversed indexes of the components. That means swapping the contents of pairs with bit-mirrored index, if we want to recycle the array x[n]. While doing this, we should avoid swapping content of entries on the identity diagonal (optional), and avoid swapping content twice (obligatory).

Let us take a look at the bit-reversed permutation matrix for N=8. Four entries are on the identity diagonal, and we would prefer to skip these. Only two pairs have to be swapped. x[1] with x[4] and x[3] with x[6].

Iterating over n, how do we decide whether to swap contents or not? Well.... if n=nrev we have an identity, and we can skip the swapping. And if n>nrev we will skip as well. Then we are sure that a pair is only swapped once. For this to work, we have to compute all nrev, even for the cases where we do not take action. Redundancy again. So be it. Let us for the moment just check whether a test routine will give correct output.

We need a loop iterating over n, and within that, a loop which computes nrev. A conditional check will tell whether the swap shall be performed or not.

I have checked that this code does the job. It may be utterly inefficient, but at least I now have a basic understanding of bit-reversed permutation. I just needed to go through this, before checking more advanced methods.

While staring at the bit-reversal matrices (I have bigger ones that do not fit on this page) I stumbled upon the 'not-identity-diagonal'. It is perpendicular to the identity diagonal, and the column index is the bitwise negation of the row index. All bit-reversed pairs seem to be mirrored over this not-I diagonal. Actually they are 180 degree rotations within the matrix. That means, once you have a bitreversed pair it is easy to identify the corresponding bit-wise-not pair that must be swapped as well.

Straightforward exploitation of this symmetry could save half of the iterations and bit-reversal computations. The illustration below shows where the bitreversed values and the bitwise negated values are located for n<nrev and n<~nrev. Iterating over n till only N/2 will suffice to compute the swaps for the whole matrix. There is one condition however: no entries should be precisely on the not-I-diagonal. They would be swapped twice if they are included.

I wrote code for this, but it turned out that it only works for N being an odd power of 2. For an even power, some entries are on the not-I-diagonal apparently. I was disappointed with the keen yet inconvenient modification.

Still, it was a stepping stone to a more fruitful reorganisation of the loop. After gazing at my permutation matrices a couple more times, I finally perceived the decisive pattern. The lower-left and upper-right quarters are coupled, while the upper-left and lower-right quarters are mirrored. They ask for separate treatment.

The upper left quarter entries must be checked against double swapping as the bitmirrored pairs are within the region itself. Furter, the identities are here. But then, once a bitmirrored pair is found and checked, the bitwise negation of it can be done simultaneously, thereby covering the lower right quarter.

The lower left quarter has it's bitreversed counterparts all in the upper right quarter and never in it's own region. These entries can be swapped unconditionally, since it happens to be the case that all the lower left entries have n=odd.

Further, it is very easy to create an odd bitmirrored pair from an even pair or vice versa. Therefore, we only have to find half of the bitreversed pairs inbetween n=0 and n=N/2. That means, N/4 iterations over the outer loop will suffice, N/4 bitreversal computations, and N/4 conditional checks. Now we are getting somewhere.

Computing bitwise-not of n can be done in C with ~n but it must be masked by bitwise-and: (~n)&(N-1). It is also N-1-n (for N being a power of 2), and n^(N-1) which is an exclusive-or.

Of this I have a decrementing version as well:

This modification speeds up the routine by a factor two, according to time profiler results. I would think there is still more gain possible.

Generally, a permutation routine would compute the bitreversed values as a running sum, rather than starting from scratch in every iteration over the outer loop. The result can be updated with helper variables of some sort. Unfortunately, the inner mechanism of such code is hard to follow.

It would be more elegant to decouple the bit-mirrored pairs from the loop index, and compute both as running sums in a symmetric fashion. The beautifullest algorithm that I have seen so far, does exactly this. It is invented and published by Jennifer E. Elaan. See: http://caladan.nanosoft.ca/index.php.

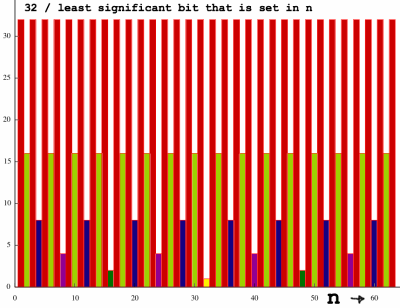
At the heart of Jennifer's technique is a Gray code generator. That is supercool! The trigger for such a generator is hidden within a natural number sequence. Below I have plotted the pattern of the trigger or toggle for N=64. Every value is a pure power of two. This universal pattern can be extracted in various ways. Illustrations of bit-patterns and extraction are on the page Bitwise&Poundfoolish.

When N/2 is divided by the values in the plot above, you get the bit-reversed values, as plotted below. It is a multiplicative reflection.

Using these patterns you can toggle-switch bits of variables initialized at zero, one at a time. That is done by exclusive-or. Then you get a Gray code sequence and it's bit-reversed version. A Gray code sequence plotted looks like this:

It looks freaky. But now watch the pattern of it's individual bits plotted, like it was done earlier for a natural sequence:

And here is the Gray code with it's bit-patterns reversed:

Despite the differences between Gray code and the 'powers-of-two' binary sequence, there is also a striking resemblance. The bits appear in blocks of sizes proportional to their value. For several reasons, both sequences work equally well in my odd-nodd-skippy permutation structure that was described earlier.

Bitmirrored pairs can now be computed as running sums with help of a loop that counts trailing zero's, a count which coincides with the base 2 logarithms of the 'toggle' pattern values. Iterating over a natural index sequence i, I add an extra shift in the reconstructions to derive even values of the forward variable exclusively. The initialisation of forward and reversed is adapted to the decrementing direction of the loop.

Another factor 1.5 speed gain is the result of inserting Jennifer's method. It works because there are only N-1 trailing zero's over N indexes, which means 1 zero on average per index. A zero's-counting-loop is therefore not quite so demanding as a loop that reverses a whole bitpattern.

For some architectures, instructions are available for counting trailing and leading zero's. Major compilers have C extensions, giving access to such instructions. GNU has __builtin_ctz() for example. It should be faster theoretically, or not? I have checked that the function is expanded inline and it accesses Intel's bsfl instruction. But for some reason, I have no profit from it.

After all these bitwise exercises, I got more confident and finally grasped how the more traditional update of the bitreversed index works. You could say that it counts and toggles 'leading ones' in the reversed index, parallel to the flipping of 'trailing ones' in an incremented forward index. And instead of shifting the index when counting, the toggle variable is shifted rightward. The toggle can also be used as a bitmask. I have adapted this method to my particular iteration scheme, and it works just as fine:

In practical applications the bitreverse permutation will be used for complex data. For now, I am working with separate real and imaginary arrays. (I will switch to a complex datatype later.) In order to keep code transparent, I have a swap function, defined static inline.

While optimizing the bitreversal, memory access becomes more and more the factor determining processing time. After all, these samples have to be swapped no matter how. I can bitreverse-sort one million real-and-imaginary arrays of length N=1024 in some 6 seconds, on an Intel core2duo 2 GHz. That is about 6 microseconds per vector pair. That will do for the moment. I must quit this topic now. In the time that I have spent on it I could have done a zillion times zillion bitreversals with whatever wasteful routine.

At last. I can add bit-reversed sorting to my FFT routines and have intelligible output from it. I will do some plots on an upcoming page. It is cool to finally have real and imaginary output plotted. Regular analysers show amplitudes or decibels, that is fine for audio engineers, but I want to see complex numbers.