Orthogonal, Orthonormal

The page on inner product showed how vectors can be perpendicular, even when they have too many dimensions to draw them in a plane. When two vectors have inner product zero, they are perpendicular, or orthogonal as it is called. Orthogonal vectors are indispensable when transforming data between domains of signal processing. If you transform a time-domain signal to the frequency domain, you might want to alter some frequency-information and then go back to time domain. Apart from the deliberate alterations, you want a faithful resynthesis of the original signal. Therefore the transform matrices must cover the complete space, with vectors that do not overlap.

I want to illustrate a transform and it's inverse with the simplest possible example. I will abuse the 2x2 matrix of a complex multiplication because we know that is has an orthogonal matrix. But now I suggest the input is two samples of a real signal, instead of a complex number.

The output is (-0.26, 0.82). Now from this I want to retrieve my input signal. What does the inverse transform look like? In this case, it is the so-called transpose of the transform matrix: the entries are mirrored over the main diagonal. The 0.8 and -0.8 are exchanged, and there we have the transpose. With this matrix we will get the original input back.

It is perfect, and I did not round anything. What type of transform was that, by the way? It was a kind of fantasy 2-point Discrete Fourier Transform with rotated spectrum. Nothing very useful in practice. The reason I chose 0.6 and 0.8 in the example is that they form a precise unit vector. Therefore, the matrix is not only orthogonal, but also orthonormal. Without a unit vector, the example would not have worked so relaxed as it did!

Why not? If vectors with a norm other than 1 are in the transform matrix, the energy in the processed signal is altered. That should at least be compensated for the inverse transform, otherwise you would end up with a signal of different magnitude. Such compensation is not difficult. It is just a matter of scaling the transpose matrix. Let us swiftly do an example of that.

This transform matrix has vectors with norm other than 1:

To normalise the vectors, you would divide them by the norm, so divide the components by the square root of two. But if you do not normalise here, you can 'norma-normalise' the matrix for the inverse transform. Then you need to divide by the norm*norm:

We will do that here. Not forget to transpose the matrix. As you can see from the result, this method will reconstruct the original signal samples just as well.

My conclusion is: orthogonality is a must for a faithful reconstruction, but regarding normalisation there is slightly more freedom. If you want to preserve energy in the transformed data, the transform matrix should be orthonormal. But there can be reasons for choosing another normalisation type. If only you do not forget to compensate in the inverse.

Summarizing, we have done two fantasy transforms until now, with rotated spectrum and a non-representative energy-content. Why not just demonstrate a more realistic Fourier Transform? Hmmmm... we need more decimals to approach that. Let me use three decimals to represent the square root of two: 1.414. And it's inverse, 0.707. In addition, I will choose the transform vectors in such a way that the first one correlates on low frequencies and the second (alternating) one on high frequencies.

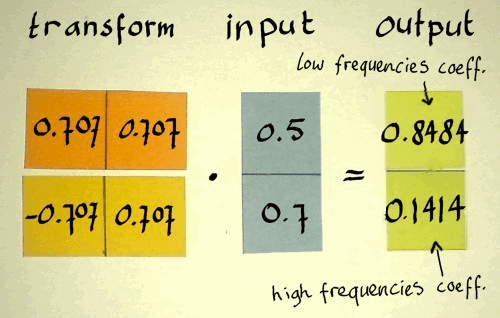And below is it's transpose. From the result it is clear that the signal's energy content is slightly reduced. That is because I rounded the square root of two, and the vectors became slightly smaller than a unit vector. With more precision in the transform vectors, the result could also be more precise. That would be a gradual difference and not a decisive difference, because very few numbers on the unit circle can be expressed with finite precision. In fact, one of these few was used in the first example.

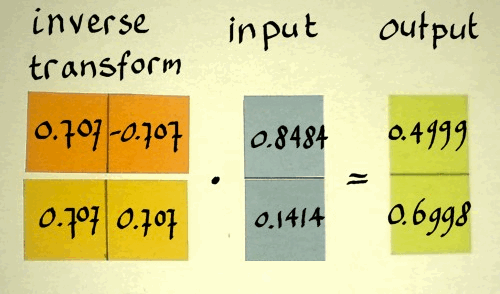Although a 2 point DFT is of no practical use because of it's poor frequency resolution, such simplistic cases can clarify important aspects. The examples showed that a transform with the poorest possible resolution may still be capable of doing an excellent reconstruction. If only the vectors are orthogonal and well-normalised. The frequency-responses of such vectors will overlap dramatically, and that may be a good reason to use longer arrays in a transform matrix. But a dramatic overlap in the responses do not prohibit a good reconstruction. Therefore, the choice of resolution does not relate to demands on reconstructibility. However, developing orthogonal matrices can be a challenge of it's own kind...