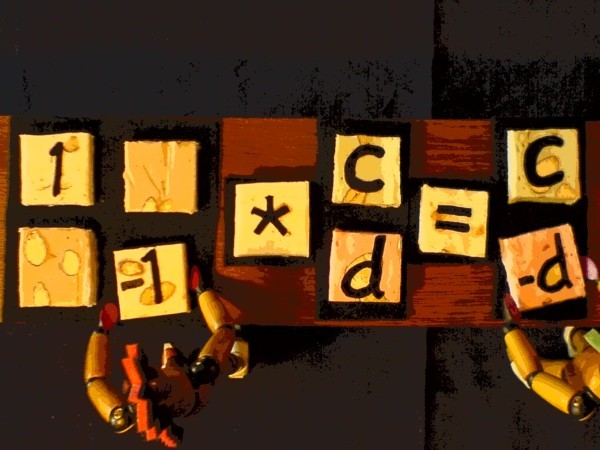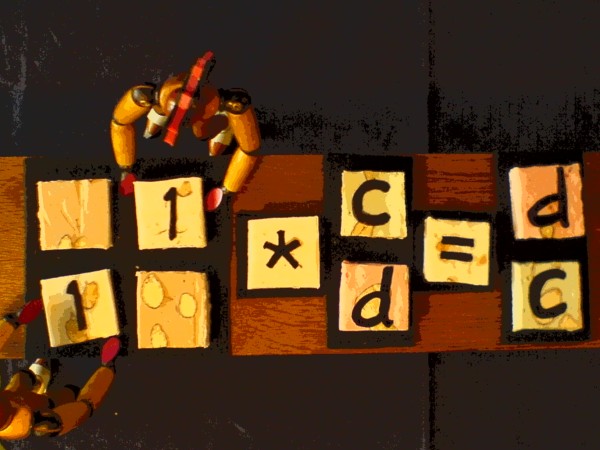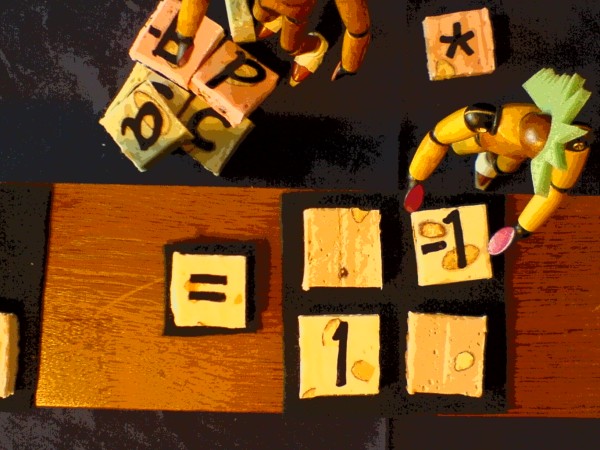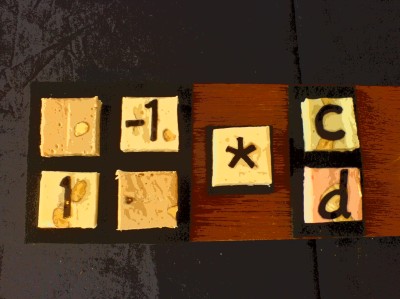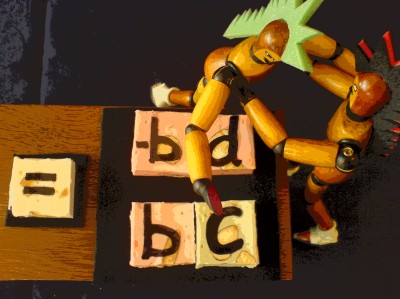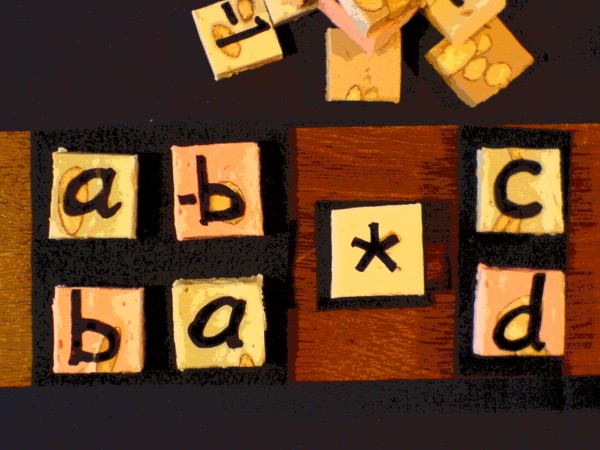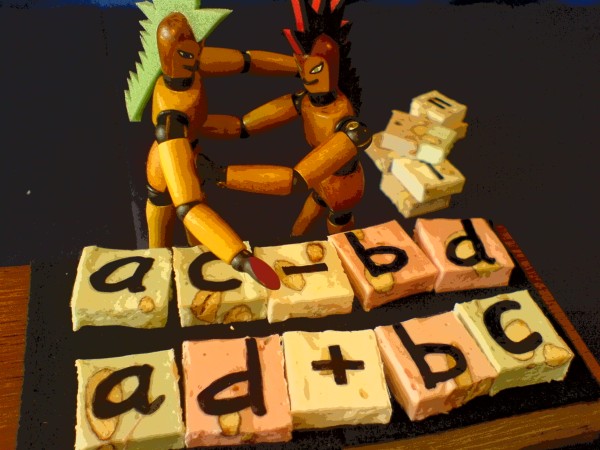Trip on the Complex Plane

Matrix View

The previous page showed how a complex multiplication (a+ib)(c+id) will result in the real product (ac-bd) and the imaginary product i(ad+bc). We will now find out how to describe this as a matrix operation. There is a parallel between the geometry of the complex plane and a matrix, which can help in understanding the rotational character of complex multiplication.

The general routine of matrix multiplication is not illustrated on this page. If you need it, goto>> ../Matrix Multiplication.

Because there are four multiplications in the complex case, the matrix operation will have this general form:

In complex multiplication, variations on three matrix archetypes are beneath the skin: the identity matrix, the permutation matrix, and the reflection matrix. I will introduce these one by one. On the left below is an identity matrix, with ones on the main diagonal. The effect of multiplying with an identity matrix is that input and output of the operation are identical.

When a constant other than 1 is on the main diagonal, the effect will be a mere scaling. The real part of (a+ib) is put on the main diagonal to produce this effect. That results in the first terms of real and imaginary products, the ac of (ac-bd) and the ad of i(ad+bc).

The scaling effect can be illustrated with an example on the complex plane. a*(c+id)=(ac+iad), where a is the scalar:

The next matrix archetype is the reflection matrix. It's effect is to reflect a vector over some axis, in this case over the x-axis.

The effect is shown in the complex plane here:

Back to the identity matrix. When it's rows are shuffled, you get a permutation matrix. In the 2x2 case, there is only one permutation scheme:

The effect of this permutation matrix is to swap the parts of (c+id):

Permutation of a vector shows like this on the complex plane:

Now we will multiply the reflection matrix by the permutation matrix:

How shall we typecast the combination? Permuflection?

Do "permuflection" on the vector (c+di):

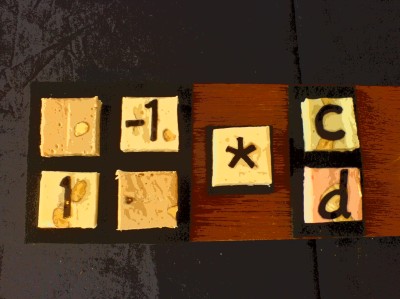
This is the result:

The values of c and d are interchanged. What is more, a plus c goes to the lower row but the upper row gets a minus d in return.

This is "permuflection" in the complex case: multiplying a vector by i. The vector is rotated anti-clockwise over pi/2 radians (or 90 degrees).

Below, we multiply with ib instead of i. This will have a scaling effect in addition to the rotation.

The final matrix of complex multiplication, with the complete vector (a+ib) in the 2x2 matrix, is this one:

And here is the result of it. Apperently i is content with his profitable position. But he may be unaware of the fact that a negative-valued c could be credited to him as well.. Generally, that probability is 50 percent.

In matrix terminology, complex multiplication is the combined systematic effect of scaling, reflection and permutation.