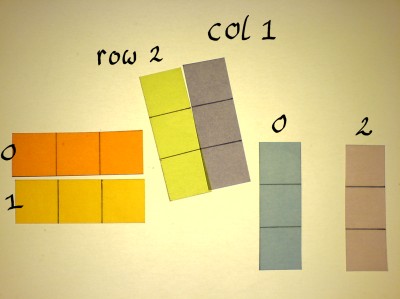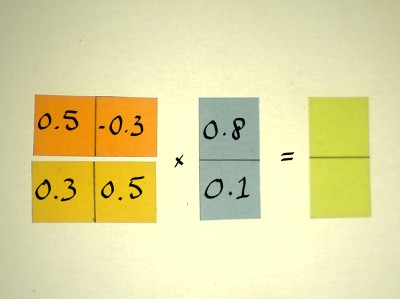Matrix Multiplication

I'm always messing up rows and columns of matrices when it comes to putting results in the proper cell. I am the type that can even screw a 2x2 matrix. The photoshoot for "Trip on the Complex Plane - the Matrix View" had to be done twice for that very reason. When you think of it: the series of row index numbers form a column. Very confusing at times. It is like the problem I have with aubergines and courgettes. Only when I see an aubergine I can tell that the green one must be a courgette. In order to supply visual support for my poor brain I've cut&pasted this page on matrix multiplication.

When two matrices shall be multiplied, the rows of the left one are correlated with the columns of the right one. I might as well cut the matrices into pieces directly. These single row and column strips are now vectors.

I give those vectors slightly different teints, to distinguish them in upcoming operations. Indexing starts with zero, at least when using matrices in dsp-technique.

Start correlating matrix A row 0,  with matrix B column 0:

Correlation of two vectors means to find the inner product: the sum of products of corresponding cells. Let us do an example.

The inner product of two vectors is just one number. That number should go in the correct cell of the output matrix. In the case of row zero, column zero, it is not so difficult to find that cell. It is just the first one we come across.

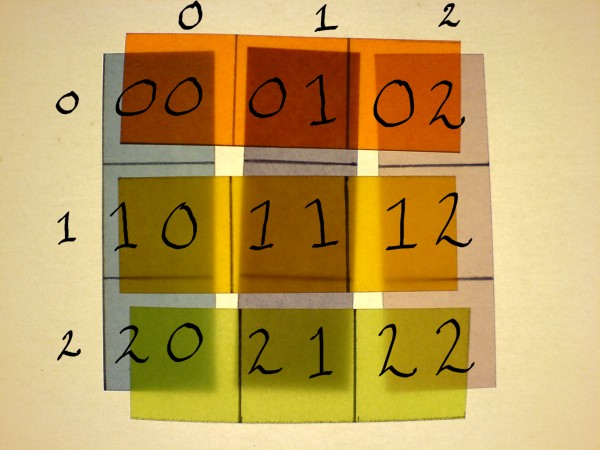
When continuing matrix multiplication, the cells of the output matrix need to be identified. By convention, the first id-number of a cell is that of it's row, and the second is that of it's column.

For example, the correlation product of matrix A row 1, and matrix B column 0, goes into cell 10 of the output matrix.

Another example, just to get the feel of it:

These examples were with 3x3 matrices everytime. But matrices need not be square. They can be rectangular, and they can consist of just one row or one column. A typical configuration is: a one-column matrix multiplied by a square matrix. The vectors must have equal length. I will do one example of that, with two-point vectors, because this has the scheme of complex multiplication.

Maybe you wonder if matrix division is also possible. In a certain sense, and under certain conditions, that can be the case. Compare with: division by 4 is multiplication by 1/4. There is no seperate operation for matrix division. Multiplication with the inverse is the only option. Provided there is an inverse, because not al matrices have one. Construction of matrices with known inverses may be in the top 3 of dsp-challenges.