Trip on the Complex Plane

Unit Circle

The third important line of reference on the complex plane, next to the axes of x and iy, is the unit circle. Well, it does not show up as a line here. It is made up of infinitely many complex numbers, all with distance 1 to the origin. These complex numbers are of special use, as they have the directest or purest relationship to angles. And angles in turn, are of use in expressing periodic motion.

If you could bend a measuring tape exactly in the shape of the unit circle, you would find..

Ah, that is hard. Normally we do not try this. But for the occasion I want to see the 'length' of this circle. Here they go:

A bit more than three unit lengths fit on half a unit circle. A more precise number can be found in a calculator. The number is called pi. The full circle would have 2pi. That is also the arc length, or angle, of a full circle. But on a circle with radius other than one, measuring would not have resulted in that number.

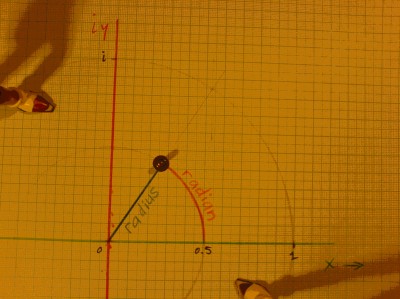
Let's do some extra pics on this. On the left is the unit circle, where you can more or less verify that both radius and one radian arc length correspond to unit length. On the right is a circle with radius 0.5, and 1 radian arc length drawn on it. One radian arc length is not a length in the sense that straight lines have, but rather a ratio of a circle or period. Only on the unit circle one radian corresponds geometrically to the scale of the straight axes.

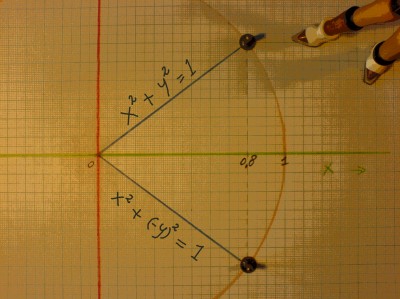
I would now like to illustrate how we can find all the complex numbers of the unit circle. Start with an example for one point: x = 0.8. How do we proceed to find iy? There must be two values for iy, as is clear from the picture.

From Pythagoras we know that the root of the sum of squares of x and y must be the radius:

We have radius 1. And because:

the sum of squares is also equal to the radius length for numbers on the unit circle.

By the way, now that we want to find iy, must we not:

????
No, this would be somewhat too zealous. Argh, I remember having one frustrating evening with that. Next morning at school I learnt that Pythagoras should be done the plain familiar way. Finding a radius length is not a complex number multiplication.

So here we will calculate two values, and once we have them they will be labeled i. First proceed to find y as the left value:

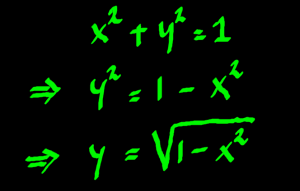These are the two functions where you can fill in any x from -1 to 1. We will now solve for the example of x = 0.8.

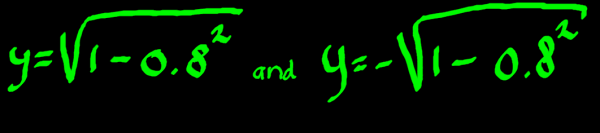No need to write the whole thing, let the calculator do the work. The answers are: y=0.6 and y=-0.6. We have found two complex numbers on the unit circle: (0.8+i0.6) and (0.8-i0.6).

If you have plotter software on your computer, you can plot the two functions and check that they each make half a unit circle. Here is a plot from Grapher, a fine utility that comes by default with Mac OSX:

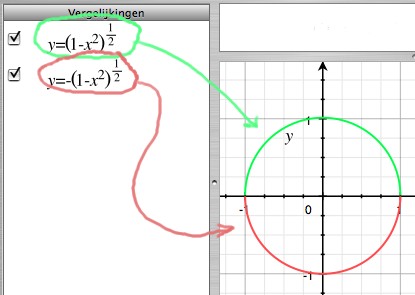Let us now make one function of it and see what will happen:

The two half circles shrink to one line segment with all y zero! Of course, the half circles have opposite sign so they cancel each other.

This is logical, but it illustrates an important aspect of imaginary parts. They often live in pairs, and can go unnoticed very well that way. Until you analytically force them to "unpair", like in complex multiplication.

So the complex numbers on the unit circle are, with -1<x<1:

Now it is time to turn to trigonometrics. It seems that x between -1 and 1 have simple complements iy, and together they make up for the unit circle. Fortunately, sine and cosine have that same complementary character. Points on the unit circle can be expressed with:

Where ß is an angle.

Why didn't I mention that earlier. That would have saved us a lot of calculations. Hmm. But I wanted to explore the unit circle as being made up of numbers. Sin(ß) and cos(ß) are functions, not numbers. They are a next step. Let us return to the one radian angle and find sine and cosine of it.

cos(1) is on the x-axis, it is a real part with value 0.54030230587 
sin(1) is the imaginary part with value 0.84147098481

The complex number on the unit circle, corresponding to an angle of 1 radian, is thus (0.54030230587+i0.84147098481).

And what about the negative side, below the x-axis? Is there also an angle of -1 radian? Yes, and it has

cos(-1): 0.54030230587 
sin(-1): -0.84147098481

The complex number on the unit circle, corresponding to an angle of -1 radian, is thus (0.54030230587-i0.84147098481).

If the output values of a cosine function are taken as the real parts, the sine and -sine values are corresponding imaginary parts. Below, these are drawn as functions of points in time x. Sin(x) and -sin(x) cancel each other, and cos(x) is the real output. This means, with real signals it is undetermined whether rotation is positive or negative. It is both at the same time.

Note that on these pages, radians are used consistently to express angles, whereas calculators can also compute and express angles in degrees, and will very often do so by default. Only when using radians, we can take full advantage of trigonometric identities. Then sine and cosine open the doorway to complex exponentials and a whole bag of tricks that can be done with exponentials and logarithms.

But how the hell can one illustrate complex exponentials with wooden puppets and a piece of p