'Real' FFT

intro

Since Fast Fourier Transform works by virtue of complex multiplication, complex signals could be transformed. In audio dsp, signals are often real only. One FFT input remains unemployed, while you can not do away with the imaginary part to reduce the count of operations. But you can 'abuse' the imaginary input and feed a second real signal in it. Since two arbitrary real signals are not orthogonal, like a complex signal is, the output spectrum is a mix which has to be split somehow.

Let me first illustrate the difference between a complex signal and a real signal. A complex signal, consisting of two orthogonal phases, has a distinct rotational direction. The spectrum of a complex sinusoid would have one real part and one imaginary part. A complex number, say (a+bi). Here is an example:

Real signals, consisting of a single phase, have no explicit rotational direction, or you could say they rotate in both positive and negative direction. Therefore, a real sinusoid correlates with two real parts and two imaginary parts.

The imaginary parts in a real signal are imaginary indeed, therefore they always add up to zero. The real parts come in a pair with equal value and equal sign, each representing half of the correlation. The spectrum of a real sinusoid has the form:

0.5(a+bi) + 0.5(a-bi)

If you would now feed that same real sinusoid in the imaginary FFT input, the correlation coefficients will simply shift by pi/2 radians. The sinusoid spectrum is then identified:

0.5i(c+di) + 0.5i(c-di) = 0.5(ci-d) + 0.5(ci+d)

The picture below shows the merged spectra as a... stack of mikado sticks. They represent:

0.5(a+a-d+d) + 0.5(ci+ci+bi-bi)

This can be distinguished as coefficients found below and above Nyquist:

below Nyquist 0.5(a-d) + 0.5(c+b)i
above Nyquist 0.5(a+d) + 0.5(c-b)i

From these we can extract a, b, c and d:

a = 0.5(a-d) + 0.5(a+d)    (real below Nyquist + real above Nyquist)
b = 0.5(c+b)i - 0.5(c-b)i  (im. below Nyquist - im. above Nyquist)
c = 0.5(c+b)i + 0.5(c-b)i  (im. below Nyquist + im. above Nyquist)
d = 0.5(a+d) - 0.5(a-d)    (real above Nyquist - real below Nyquist)

The values of a, b, c and d represent coefficients for the positive frequencies in (a+bi) and (c+di). From them, we can compute their conjugates. These follow the normal principle of real coefficients having equal value and sign, where imaginary parts have equal value and opposite sign. Two index points have no conjugates: harmonic zero (DC) and harmonic N/2, the Nyquist point. Since the Nyquist point is midway between the positive and negative frequencies, it can be computed within the routine for the positive and negative frequencies. The index is then N/2 for both positive and negative. But DC has to be computed separately, because point N does not exist. Below is how you could do such a thing in C code. For simplicity, I do not multiply with 0.5, because this can also be compensated for in a regular normalisation of forward transform.

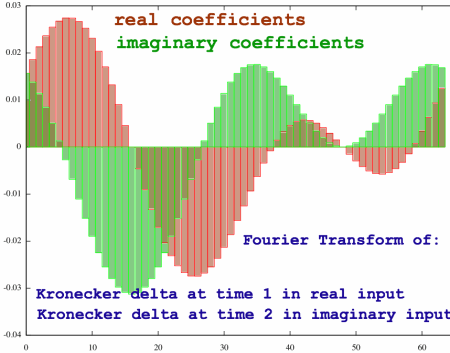
Below is an example of two merged spectra that we are going to split.

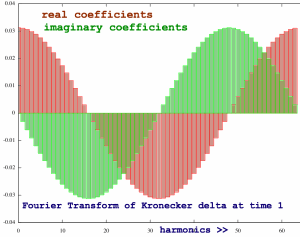
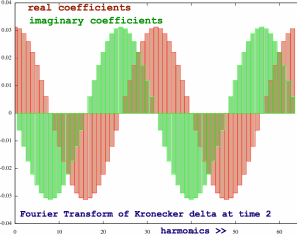
Splitting the spectra with the code described above, two familiar patterns arise:

Apparently I forgot to modify the normalisation, and indeed the coefficients have twice the normal weight. Anyway, all theory is confirmed by this result.

For inverse FFT, we have to merge the two spectra into one spectrum which is transformed by an inverse complex FFT. The signals appear at the real and imaginary FFT outputs. Merging the spectra is simply the inverse process of splitting: reverse the equations. It took me quite some time to get it right, but the operations are very simple again.

To compensate the doubling of the correlation magnitude, I have adapted the 'normalisation' factor in my forward FFT. Normally I have this factor at 1./N and now it is set to 0.5/N. This arrangement saves quite some multiplications, but you must not forget to include the Nyquist point in the computations of split and merge. This coefficient will only get the correct value when it is treated like the other points. In the inverse transform, no further normalisation factor is needed. The signals are reconstructed with their original samplevalues.

Obviously, the procedure for splitting and merging can be further optimized. For example, computations could be done partly in place, using two real and imaginary arrays instead of three. But I will skip all that, since feeding two real signals in one complex FFT is not the final goal. The whole purpose of this page was to introduce the topic of real FFT at a slow pace. The next step is much more complicated: how to cut a real signal in two parts and process it with a complex FFT of length N/2. That is for the next page.