spectfilter~ object

After prototyping a parametric Fourier filter in a Max/MSP patch, I developed C code for that process, which can be found at the bottom of this page. Combined with the FFT lib I had written earlier, it is plugged into one single Max/MSP external object for further testing, demonstration and musical employment. The object description is followed by links where you can download the object or a demo application.

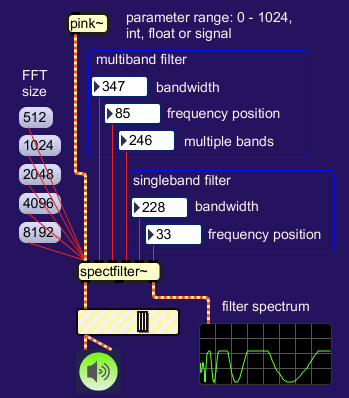
The most significant improvement in the single-object implementation is a user-controllable FFT size in runtime. Since the resolution/latency trade-off demands a choice of FFT sizes, according to programme material, this really was a requirement for the new object. In addition to the multiband filter as described on the previous page, the object has an extra single band filter spectrum, in serial connection. It's function is to confine the multiband output to a specific region of the spectrum, if so desired.

In it's simplest form, a patch using the spectfilter~ object would look like this:

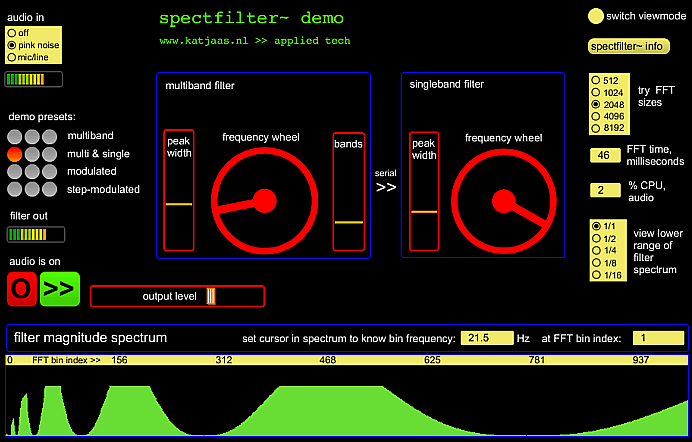
Round the spectfilter~ object I figured a test/demo patch, where the object is submitted to intense manipulation by modulators. Next to audio output, the object provides filter spectrum index and y-value, which in the demo patch are employed for meticulous visual inspection.

The test input signal is pink noise, but mic/line signals are of course also enabled, because they were the reason for doing spectfilter~ in the first place. It turns out that the object can fluently reflect the weirdest of modulations, extending it's musical versatility beyond static filter jobs.

In the demo patch, the filter spectrum is dynamically stored into a named buffer~ object which is viewed via a waveform~ object. This way, the action of the filter can be scrutinized in realtime, much more detailed than with a scope~ object. Settings are available to zoom in on the lower spectrum range, where things are more critical than higher up. The lowest octave interval in a discrete spectrum comprises only one FFT bin, one sample, while the highest octave has half the total spectrum width. Below, the lowest 1/16 portion of a multiband filter spectrum is represented, for a 2048 point FFT. The bars represent individual FFT bin values:

Because of the relatively artefact-free resynthesis routine, such narrow filterbands are not directly problematic, soundwise. The blocky shapes could make you suspicious, but overlap and proper windowing of FFT frames will make a smooth filter curve out of this, no matter how discontinuous it may look. The real hassle is, that filterbands comprising just one FFT bin or even less, can no longer correctly represent logarithmic bandwidth and distribution.

On the page Fourier Filter, I had made the assessment that logarithmically distributed separate filterbands can be computed with sufficient accuracy around bin 30 and higher. From my animated filter spectrum I can now see that this is indeed the case. My desire to make filterbands extremely narrow complicates things further. The figure below does not even show the narrowest filterband setting in spectfilter~, but even here it is clear that bands below bin 30 are totally beyond control, due to lack of resolution:

The figure also shows the frequency at bin 30: 646 Hz. (I set the cursor in the spectrum representation to request the frequency for a bin). So, everything below that frequency can not properly follow the logarithmic scheme. For smaller FFT sizes, things are worse, while for larger FFT sizes it's better.

From these figures, you would say that the spectfilter~ object is pretty useless in musical practice, uh? I had hoped for a method to refine a spectrum's resolution by upsampling. Then I met with the Stretchable but Indivisible Dirichlet Kernel that is the discrete Fourier transform of a pure sinusoid. Upsampling refines the analysis, but can not help with sharper filtering. This is the relentless reality of spectral filtering. Details on this topic are on the page Windowing & Frequency Domain Filtering.

Despite this ever-present bottleneck at the low frequencies, spectral filtering has it's attractions. Specially when you can quickly choose an appropriate FFT size for the filter job at hand. Below is an example with two filter lobes, done with 512 point FFT (that is 11 milliseconds at sampling rate 44K1):

If you want to chop your input signal into a couple of dozen peaks, set a long FFT. Though resizing the FFT can even be done while audio is on, increasing the size (thus increasing latency) will introduce a short moment of silence, so you still have to choose an appropriate moment for the switch. The filter spectrum shown below, done with FFT size 8192, could not so easily be applied with time domain filters, certainly not at the price of just a couple percent CPU time:

Such filter settings effectuate specific musical effects. With noisy input, the filter becomes an instrument in it's own right. And since the filterspectrum is so easily recomputed, to the point of continuous modulation, spectfilter~ could be exploited in electronic music composition indeed. That is not what I made it for, but the lines between sound processing and synthesis are very thin here.

circular spectrum

In the spectfilter~ object, the filter spectrum is handled as a periodical phenomenon. This enables a continuous shift of filter peaks towards the low end or high end of the spectrum without ever reaching a limit. The peaks just wrap around. The effect is reminiscent of the famous Shepard tones, but with spectfilter~ the sound can be pure or diffuse, depending on filter settings.

To optimally exploit this unbounded filterband shifting, I had to find a method which can handle automated shifting and manipulation by hand simultaneously. Something like a turntable, where you can play around with speed and direction of the machine. Conveniently, Max/MSP has a dial object that can do full circles of 360 degrees, with circular mouse tracking. Ideal for this purpose. For Max fans, here is a patch and explanation:

The essence is in diffentiating the output values of a sawtooth modulator wave (phasor~), and with these values, increment/decrement an integrator which is built around the graphical interface object. That integrator must wrap to zero after reaching the maximum parameter value, which is 1023 in my case. This can be realised by using a bitwise-and mask, but only when the parameter is of unsigned integer type and it's maximum value + 1 is a power of 2. Anti-clockwise wrapping is also possible, if a constant addition of maximum value + 1 is included in the loop.

The cyclic nature of frequency position applies to multiband and singleband filter in the spectfilter~ object. The other parameters controlling bandwidths and number of filterbands do not wrap around. Parameter values run from 0 till 1023 inclusive and are 'dimensionless', they do not mean anything physical. It is just one of many standard parameter ranges, and my personal favourite.

If you are on Intel Mac, you can play around with spectfilter~ yourself. The object is available, together with the demo patch in the form of spectfilter~.maxhelp. If you do not own Max/MSP, you can download spectfilter~demo.app, which has Max Runtime built in. Max 4.6 users could download both zip files, one for the object and the other for the demo, since spectfilter~.maxhelp was created in Max5 format.

downloads

Part of the spectfilter~ object is a C function that computes a filterspectrum with logarithmic shape and distribution of filter lobes, shown below. It is a refinement of the procedure outlined in the prototype patch on the previous page. The minimum bandwidth is no longer a function of actual FFT size, but a function of the maximum FFT size permitted by the object's buffers. This helps in keeping filter characteristics uniform across FFT sizes. The object incorporates FFT and window/overlap functions which are not shown here. Separate pages on these topics are in the FFT section.