<<home <<previous next>>

Bitwiser FFT

The previous page showed a plain FFT routine, quite literally derived from matrix illustrations of Fast Fourier Transform. On this page, I will redo that routine using some bitwise shortcuts that I have found since then. Not all of these modifications are intended to make the routine faster. It is more about exploring possibilities.

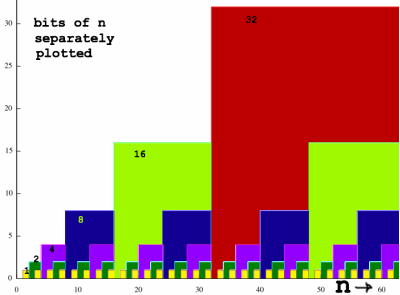
The basis for the bitwise operations is the bitpattern in the indexnumbers of an array with length N = 2^x, x being a positive integer. I have plotted the individual bits in a natural sequence to visualise the pattern:

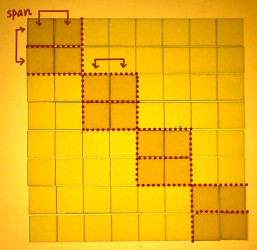
The bitpattern corresponds to patterns in the FFT stages. Let me try to illustrate this. For my N=8 example, the first stage has the following pattern of entries that must be combined. The first half is a 4-point block where the 'span-bit' is lo, the second half is a 4-point block where the 'span-bit' is set. The span-bit is binary 100 and has decimal value 4. I have written the indexes of the input array in binary to clarify what I mean with the 'span-bit' being lo or set:

In the second stage, the pattern is that of 2-point blocks where the span=2 bit is alternating lo and set.

And of course this pattern extends to the last stage as well, where the span-bit is 1:

The span variable is a pure power of two in every stage. We could call the alternating blocks: zero and one, even and odd, or lo and set. Here is an impression showing the blocks as being the bits of a natural binary sequence:

For radix 2 FFT with larger N, the pattern will expand in a systematic fashion. The span variable regulates the flow of operations in my basic FFT implementation to a great extent. After playing around with bitwise methods I found still more employment for span. One level of branching, the loop over the submatrices, can be replaced by a simple instruction to run over even or odd blocks exclusively. Let me illustrate how to iterate over the odd blocks.

Normally, an index of a loop is incremented with 1, writing n++ in C code. We replace the index variable n with odd because we are going to iterate over the odd block components. The regular increment now reads odd++. To make shure that iterations go over odd blocks exclusively, write an extra odd|=span after the regular increment. That is an inclusive-or. Index numbers with the span-bit low will be skipped, they simply can not exist.

To find the even part of the dual node pair that must go with the odd part, write: even = odd^span. This is exclusive-or and it will switch the span-bit off. Summarizing:

odd++; // normal increment
odd |= span; // always set the span bit for odd
even = odd ^ span; // clear the span bit for even

This is not the only option but it makes for the simplest adaptation of my previous scheme. Before rewriting the code, I will discuss another modification: a look-up table for the trigonometrics.

Recall that we need complex Nth roots of unity for the rotations, the so called twiddle factors. Actually, because we work with aliases on the unit circle, we only need half a cosine function and half a minus-sine function. Here is a picture from the earlier pages to refresh:

A separate function can be written, which is called once in main, to fill arrays realtwiddle[n] and imtwiddle[n] with real and imaginary parts of the roots of unity.

void rootsofunity(double *realtwiddle, double *imtwiddle, unsigned int logN)
{
double twopi = 6.28318530717959;
unsigned int n, N;

N = 1<<logN;

    for(n=0; n<(N>>1); n++)
    {
       realtwiddle[n] = cos(twopi*n/N);
       imtwiddle[n] = -sin(twopi*n/N);        // do not forget minus sign
    }
}

In the FFT routine, the twiddle factors must now be found by their indexes. I will declare a variable 'rootindex' for that purpose. In the first FFT stage, the indexes 'even' and 'rootindex' coincide. But in later stages the frequencies increase and the indexes do not coincide any more. We must run faster over the arrays with roots. This can be done with help of a variable that starts at zero and is incremented by one for every stage. Let me call this variable 'log', as I will use it as a base 2 logarithm, and bitwise shift the even index with it. Further, the rootindex shall never exceed N-1. The modulo 2pi wrap was formerly secured by the sin and cos functions, but now we are responsible. It is fixed by bitwise-and masking. The code will look like this:

rootindex = (even<<log) & (N-1);

From the description the impression could arise that we have a lot more variables now, but actually the opposite is true.

void fft(double *real, double *im, double *realtwiddle, double *imtwiddle, int N)
{
    unsigned int even, odd, span, log, rootindex;    // indexes
    double temp;
    log=0;

    for(span=N>>1; span; span>>=1, log++)
    {
        for(odd=span; odd<N; odd++)         // iterate over the dual nodes
        {
            odd |= span;                    // iterate over odd blocks only
            even = odd ^ span;            // even part of the dual node pair

            temp = real[even] + real[odd];
            real[odd] = real[even] - real[odd];
            real[even] = temp;

            temp = im[even] + im[odd];
            im[odd] = im[even] - im[odd];
            im[even] = temp;

            rootindex = (even<<log) & (N-1); // find root of unity index
            if(rootindex)                  // skip rootindex[0] (has an identity)
            {
                temp=realtwiddle[rootindex]*real[odd]-imtwiddle[rootindex]*im[odd];
                im[odd]=realtwiddle[rootindex]*im[odd]+imtwiddle[rootindex]*real[odd];
                real[odd] = temp;
            }

        } // end of loop over n

     } // end of loop over FFT stages

} //end of function

What is the advantage of the 'jump-over-the-even-blocks' method? In an FFT, there are ²log(N) stages, N-1 submatrices, and ²log(N)*(N/2) dual node pairs in total. That means, I traded N-1 submatrix iterations for ²log(N)*(N/2) extra instructions. Sounds like a bad deal. The workflow is better streamlined however. The amount of iterations over the inner loop is fixed at N/2 in each FFT stage. The inner loop can be unrolled to an extent of choice, eventually reducing overhead of branching.

Just for fun, I also figured out a decrementing version of the above. Iterations would then go over the even blocks exclusively. From even, find the odd-block value for the dual node pair, by setting the span bit high. From there, the even value is redefined by clearing the span bit. Notice that even[0] and odd[span] would not be computed unless the traditional decrement is placed within the curly brackets, and the initialisation of even is altered accordingly (otherwise it would be even=N-1-span).

....

for(even=N-span; even;) // inner FFT loop, no decrement on this line
{
    even--;              // traditional decrement at a non-traditional place
    odd = even | span    // set span bit in odd
    even = odd ^ span    // clear span bit in even
....

It may seem odd to set a bit and then clear it again, but initially you do not know the status of the bit and this is the easiest way to have control. Juggling around with loop indexes this way is quite delicate and can easily result in illegal index values or endless loops. But once everything is set correctly, it should be reliable like a conventional loop.

The last stage of my FFT routine contains no twiddles. With this stage peeled off the outer loop, it can eventually do normalisation instead of twiddling.

....

for(log=0, span=N>>1; span>1; log++, span>>1) // loop over FFT stages
{
......// code as in previous example
}
// loop will end before last stage

// last FFT stage has normalisation, no twiddling

double norm = 1./N; // normalisation variable

for(even=N; even; )
{
     even -= 2;                // attention, decrement at unusual place
     odd = even|1;

     temp = real[even] + real[odd];
     real[odd] = (real[even] - real[odd]) * norm;
     real[even] = temp * norm;

     temp = im[even] + im[odd];
     im[odd] = (im[even] - im[odd]) * norm;
     im[even] = temp * norm;
}
// end of last FFT stage

Notice that the normalisation type is a matter of choice. It can be different from 1./N, depending on the transform purpose. I have done a separate page on that topic, Normalisation Matters.

This leads me to another question: how to derive the inverse FFT? Apart from normalisation matters, there is also the question of the reversed rotation in the inverse transform. The imaginary twiddle factors should be sign-inverted, that is easy enough. But when I started figuring out a bitwise solution for that, I stumbled upon a surprise, which is described on the next page.

^top <<home <<previous next>>