FFT window and overlap

I got interested in FFT window types when designing my parametric Fourier filter, which is supposed to do extreme filtering in frequency domain. The filter seemed to benefit from windowing and 4 times overlap of FFT frames. My ears were convinced, but why and how does it work? On this page I want to figure that out in detail.

Windows are designed to reduce the problem of spectral leakage. Leakage occurs with every frequency component that is not harmonic with the FFT fundamental. The correlation for such an inharmonic sinusoid will spread over all bins. There is a peak and a base in the spectrum of this sinusoid, but the contour can be manipulated by applying one or the other window type. Window functions are multiplied with the FFT input signal. They modulate that signal, thereby altering the leakage character of the analysis.

Using no window whatsoever is equivalent to a rectangular window, which multiplies the input signal with 1 at all indexes of the FFT frame and 0 elsewhere.

A simple smooth window function is the Hann window (named after Julius von Hann), and it looks like this:

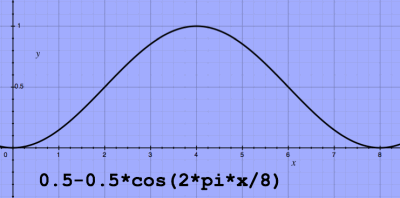The function is identical to sin²(pi*x/8).

Intuitively, I would think a window should be symmetric. The plot looks symmetric at first sight, but here, as so often, a one-sample-complication pops up. Should the Hann window be defined 0.5-0.5cos(2*pi*x/N) or 0.5-0.5cos(2*pi*x/(N-1))? I found both (amongst even more) definitions, from various sources. Following the first formula for N=8, the eight discrete samples of the window function can be plotted at indexes 0 - 7:

That is not symmetric! So let me try the second formula, with N-1 as the divisor, for the same N=8 case:

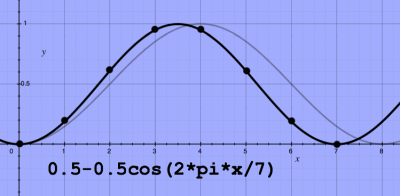Now the window is symmetric. But it does no longer have the FFT's periodicity. Despite my initial preference for a symmetric window, I now tend to believe it should rather match the FFT's periodicity than be symmetric. We will encounter some arguments for that later on. Below, the terms of the (non-symmetric) window are plotted separately:

Both terms are frequency components of the Fourier matrix proper, and analysing an N-point Hann window with an N-point DFT, the spectrum magnitude coefficients are:

x[0]    0.5   (DC)
x[1]   -0.25  (fundamental)
x[N-1] -0.25  (conjugate of the fundamental)

The window function 0.5-0.5cos(2*pi*x/N) can also be identified as: 0.5+0.5cos(2*pi*(x+N/2)/N). Written like that, it shows up as a time-shifted version of a window centered round zero. With time zero at the center of an FFT frame, the window's cosine component is at zero phase and thus positive:

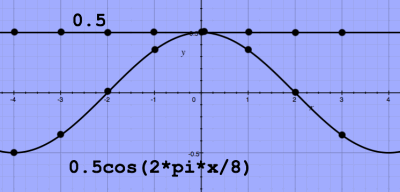The sum of these terms is equal to cos²(pi*x/8), and the Hann window is sometimes called squared cosine window. In terms of frequency components, very few windows are simpler than Hann's. But is it effective? Before running this and other windows on test functions, and analyse effects, I need to raise another (in retrospect quite naive) question.

Since a window is actually an amplitude modulation of the FFT input signal, must we not demodulate after reverting from frequency domain to time domain, to restore the signal? The focus in text(book)s is always more on analysis than resynthesis. Till now I have seen very little comment on this, and the following it just my guess.

It seems to me that demodulation or de-windowing is impossible with a window like Hann's. Since the function has some very small values and even a zero, the multiplications can not be inverted. So, should we use a different window type in case of FFT/IFFT jobs? Like the Hamming window, defined 0.54-0.46cos(2*pi*x/N), which has larger values at the extremes? In that case, demodulation would be an option. But must we demodulate anyway? Generally, FFT/IFFT is done with window&overlap. With 2 times overlap, and using the (non-symmetric!) Hann window, the sum of the overlapping window functions is exactly 1 everywhere:

The constant sum implies a proper reconstruction of the signal after IFFT and summation of the overlapping frames. This will not be the case with the 0.5-0.5cos(2*pi*x/(N-1)) formula. So that could be one reason to use a non-symmetric window function.

The constant sum arises from the fact that a cosine function has a mirror-symmetry in the vertical direction. Adding more cosines of different periodicity to the window function will make it sleeker and disrupt the vertical symmetry. Below, two-times-overlapping Blackman windows are plotted, with formula 0.42-0.5cos(2*pi*x/N)+0.08cos(4*pi*x). The sum of these is not a constant at all:

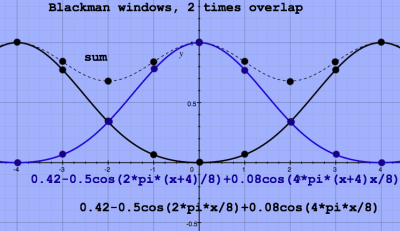The fluctuating sum translates in amplitude modulation of the reconstructed signal after IFFT. Theoretically, this modulation could be undone after summing the reconstructed frames. But it would mean that certain portions of the complete signal have less weight in the analysis than others, that's not fair.

When four-times-overlapping Blackman windows are plotted, and the sum of these, a neatly constant sum appears again:

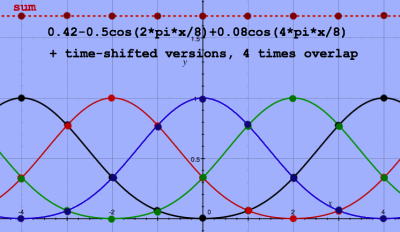From these plots I can understand why some window types can not be used with two times overlap, and require four (or maybe even more) times overlap.

The particular windows I plotted so far had only a few cosine terms, meaning a few spectrum coefficients. But, analysing or using the window function within an FFT frame, the few-term function is actually multiplied with a rectangular window! The spectral effect of that can not be seen when the periodicity of the window matches that of the FFT fundamental. But for shure there is a spectral difference between an infinite length cosine function and a function that is zero outside the interval 0 - 1. To get a more representative spectrum of the window, it should be analysed together with a lot of these zero's.

Below is a spectrum plot of a 16 point rectangular window analysed with a much wider FFT, 1024 points.

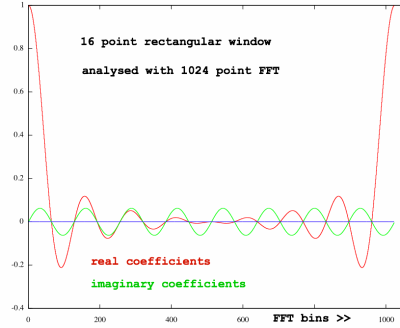The rectangular window has the function cos(0), being all ones, over the 16 point interval, and zero elsewhere. Analysed with a 16 point FFT this would give just one spectral coefficient, the DC component. But now, analysed together with many zero's outside the window, we get a more realistic impression of it's spectrum.

At this point in my experiments I happened to read Frederic Harris' excellent article 'On the Use of Windows for Harmonic Analysis with the Discrete Fourier Transform'. From this, I learned that the shape of the above spectrum is particular, and it has a name: Dirichlet kernel. It shows similarity to a sin(x)/x function, but it is periodic.

Without knowing it's name, I already encountered the Dirichlet kernel when multiplying and summing the complex roots of unity, which are part of the Fourier matrix. When more and more harmonic cosines are summed, the result starts to approach a pulse wave with the periodicity of the fundamental cosine. The Kronecker delta 'function' is the ideal pulse, in digital domain existing as a single value 1 amidst zero's. While the Kronecker delta's Fourier transform results in a flat spectrum, a sequence of ones, constituting a rectangle function, has a Dirichlet kernel as it's Fourier transform. When the ones completely fill up an FFT frame, the Dirichlet-shaped Fourier transform is no longer recognised because the zero's of the Dirichlet function exactly coincide with FFT bin locations, as is indicated here:

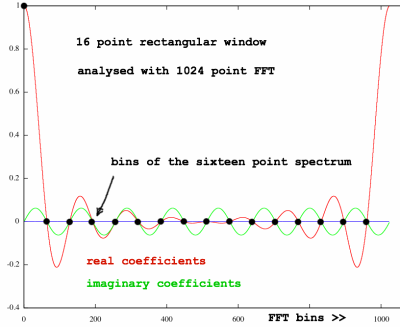When reading about FFT windows, I always wondered how they got those window spectrum plots with all the so called sidelobes. So now I understand that at least you have to analyse a window in it's context of surrounding zero's. It is even more fun to analyse the constituing terms of a window, as I have learned from the Harris article. It shows how the terms cooperate by phase cancellation to create the desired effect.

Below is a spectrum plotted, of a cosine function with the fundamental periodicity of it's 16 point frame, and analysed with 1024 point FFT. Such a cosine function, with certain amplitude over the interval -N/2 till N/2-1, is a term in many window types . Like the rectangular window itself, by the way, in it's appearance of framed DC component, constant, cos(0) or whatever describes a straight horizontal line.

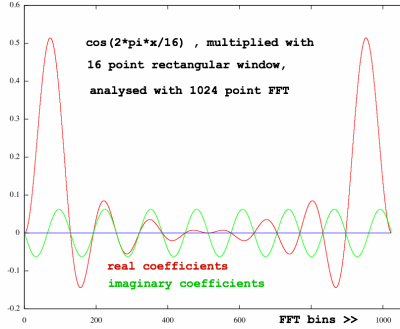Is this also a Dirichlet kernel? Hmm.. not precisely. I normalised with factor 64 for the larger FFT size, but look, the peaks are not at 0.5, they are slightly higher. That makes me suspicious. Let me plot the correlations for positive and negative frequencies separately (they are both normalised with an extra factor 0.5 for this):

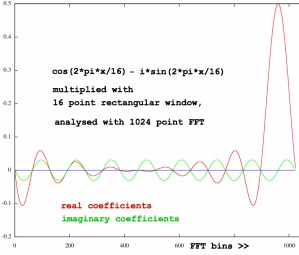They are one Dirichlet kernel shifted rightward (correlating the positive frequencies) and the other shifted leftward (for the negative frequencies). The Dirichlet kernel is periodic and therefore the shifts are really rotations. Which resulted from modulating the rectangular window in time domain. These things are common knowledge, but when plotted with these 'inter-bin lobes', it looks disturbing. Positive frequencies also correlate substantially with negative coefficients? If they are not harmonic with the FFT framesize, they will correlate with all bins - positive and negative will happily penetrate into each others' region. A complicated phase-summation and -cancellation pattern is the result.

That is also the case when summing a framed cos(0) and cos(2*pi*x/N). Let me plot the spectra of these functions in one figure, but not yet summed:

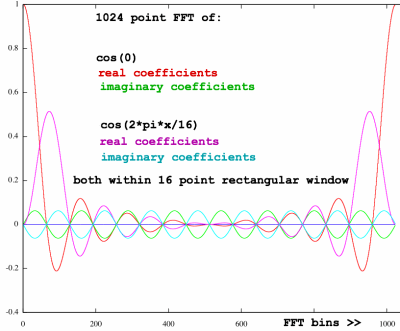It is clear that in a sum spectrum of these terms, many coefficients will cancel each other. Let me check this by plotting the spectrum of a window that is composed of these functions, each with half magnitude, the Hann window:

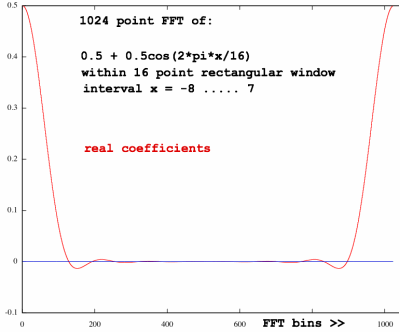Yip... that looks pretty. The real parts outside the region of the main peaks are substantially reduced. All imaginary parts, resulting from the window not being symmetric, are completely eliminated by phase cancellation. This Hann-window therefore is phase-neutral. For a window, this phase cancellation is advantageous, but it also demonstrates how coefficients can eat each other in a sum spectrum, equally so if you did want to see them.

The window-analysed-with-larger-FFT represents it's leakage character, and from there it is possible to express the character in terms of standardised  parameters. In order to better compare different window types, the y-values need to be recomputed on a logarithmic scale, so details become more pronounced. But I am not going to do that yet, because first I need to understand what the window actually does to the spectrum of a signal input.

Just as convolution in time domain is equivalent to multiplication in frequency domain, the inverse equivalence is also true. Multiplying the input signal with a window is equivalent to convolution of the signal's spectrum with the window spectrum. So, the window's spectrum is a convolution filter, acting on the input signal's spectrum, but normally implemented as a multiplication in time domain. That is one way to observe it. What type of filter does the Hann window's spectrum represent, with it's three complex coefficients at x[0], x[1] and x[N-1]? Well... we know how it looks in time domain: a smooth roll-off from x[0] to x[-N/2] and x[n/2-1]. I would say it is a lo-pass filter, which will smoothen an alternating function. Let me just try if that is correct.

Below is the spectrum of a non-windowed cosine function with periodicity 10.2 respective to the FFT framesize. I have chosen a small framesize, N=64, to better perceive an alternating tendency if present.

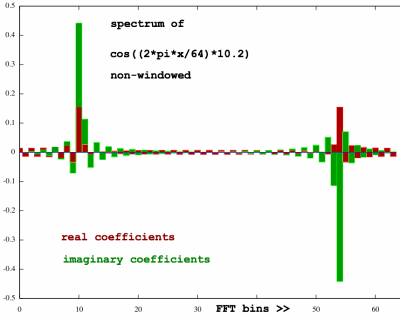Since the function does not harmonize with the FFT framesize, there is a lot of leakage visible. Apart from the central peaks, the coefficients do alternate indeed. These alternating coefficients should now be suppressed to some extent, by applying a window to the input signal:

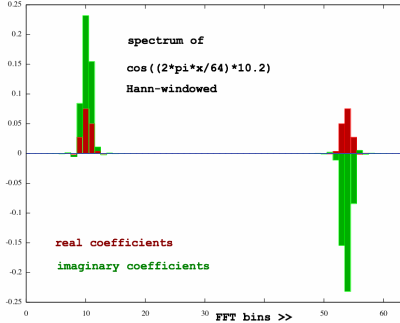Cool, that works quite OK! The spectrum is tidied up, as if the mess was shoveled up onto the central peaks, wich have grown fatter. I am kind of exited to see this at work. The window is a lo-pass filter for the spectrum indeed. Well, nothing could be more logical, considering the shape of the window, which looks like the frequency response of a lo-pass filter... Still, I was never aware of this now so obvious fact.

Why was it not obvious? In fact, I am still confused. I was doing my experiments with a zero-phase cosine function, using a time-zero centered FFT. This seems to give correct results. Maybe you have read my page 'Centered FFT'. It tries to illustrate how a N/2 shift in time domain results in alternation (= multiplication by (-1)ⁿ) in frequency domain, and how an FFT routine can be adapted to analyse an array as if it were centered round time zero. A non-centered FFT should give correct results as well, but the window is time-shifted by N/2 and it's spectrum coefficients are alternating. This must be a hi-pass filter then.

Let me check if that is the case. Here is the non-windowed cosine of periodicity 10.2, analysed with non-centered FFT:

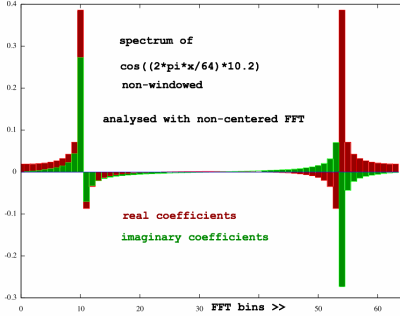And here is the spectrum of the windowed version:

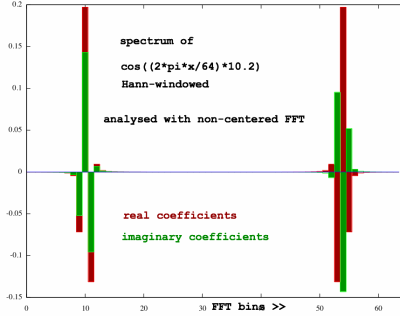High-pass filtering in the non-centered case leads to a similar effect of tidying up the spectrum. The peak coefficients are alternating, but that is just one symptom of the phase-shifts occurring with a shift in time. There is really no fundamental difference in the window's effectivity. The time-zero-centered case can still be emulated by multiplication with (-1)ⁿ. Look, this is what we get when analysing with centered FFT, but leaving time zero of the function at the start of the window. It is still the same sequence of samples as in the previous plot, but the centered FFT will see cos((2*pi*(x+32)/64)*10.2).

Although it is a matter of choice whether to evaluate over the interval starting with time zero or the interval centered round time zero, I will rather use a time-zero-centered FFT whenever possible. Time zero is the reference point for phase angles, which are in that case correctly expressed as running between -pi till pi, not 0 till 2pi like it is in non-centered FFT. Reducing the risk of misinterpreting complex coefficients, that is.

window comparison

Now that I start to understand how a window does it's job, I want to compare a couple of them. We need to see a spectrum with 'lobes', caused by an analysis frame much wider than the window. The highest peak should be normalised to 1. To zoom in on details, it shall be presented on a logarithmic scale. To compute logarithms, we must first get rid of negative values, zeroes, and very small numbers. This is done by computing the squared magnitudes and clipping small values. Since spectrum magnitudes are normally computed by doing Pythagoras on the complex numbers, I now simply do Pythagoras without the square root. That is:

(real coefficient squared) + (imaginary coefficient squared)

A good window does not have imaginary coefficients, but the rectangle window has them, so they must not be forgotten. These squares of magnitudes are then converted to deciBels with 10 * ¹⁰log(x). (Notice that this is equivalent to first taking the square roots of the squared magnitudes and then convert with 20 * ¹⁰log(x)). With the summed squares clipped at a minimum value of 0.00000001, the y-range will be from -80 till 0 deciBel, which is where most things happen. Here below is the rectangle window's spectrum plotted in this fashion. It is a Dirichlet kernel in logarithmic disguise:

Most authors produce spectrum plots with frequency zero in the center. So far, I did not follow this convention, but now I feel tempted to do so. It then makes more sense to speak of 'main lobe', 'side lobes', as is regularly done, and we will get the familiar phallus-like figures. So here we go:

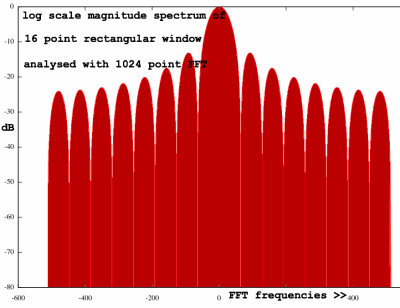The sixteen point window shows fifteen lobes, since there is no dip at frequency zero.

The way to interpret the figure is: for any frequency bin in a windowed FFT, an important part of the correlation is in the main lobe, while another share is distributed over the side lobes. Only when the analysed frequency harmonises with the FFT size, the leakage falls precisely inbetween the lobes. Although the analysis of window functions is by convention centered round frequency zero, a similar pattern will hold for other bin frequencies, since that is in fact a matter of modulating the window. You will get one peak for each conjugate, and the pattern can be distorted by phase effects, as I will demonstrate later.

Here comes the Hann window spectrum, the one that was used in the experiments higher up.

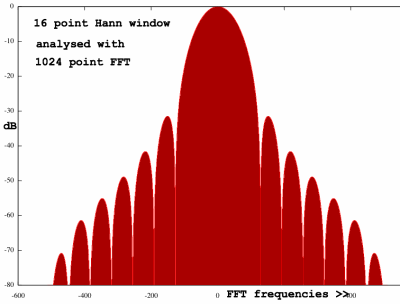The central lobe is fatter. The sidelobes are thinner and, more important, lower in deciBels, as compared to the rectangular window. It is the shovel-effect, but now presented in a standardized format.

Next is the praised Blackman window, with definition:

0.42 - 0.5cos(2*pi*x/N) - 0.08cos(4*pi*x/N)

This one spills very little energy outside the main lobe. There is a 58 dB difference from the central peak to it's direct neighbours. In return, the main lobe has grown really fat, which makes it harder to resolve frequencies that are near to each other.

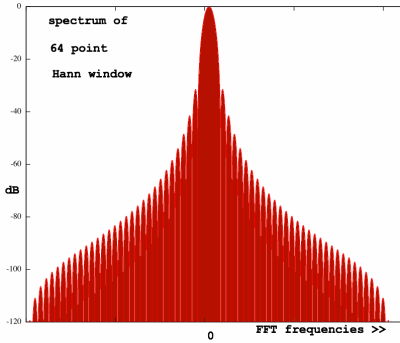
16-point window spectrums give a detailed impression of what happens round the main lobe, but real life FFT's are regularly much larger, so we also want a view of what happens beyond. I chose to inspect the same window types but now with 64 points and on a 120 dB range.

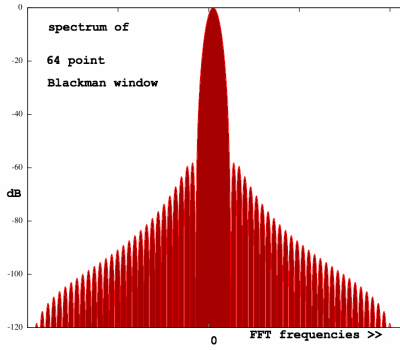The main-lobe-fatness, as related to unit window points, is not dependent on window size. Neither is the dB distance to the first sidelobe peaks. Therefore, window characteristics are unambiguous.

The sidelobes of a useful window do not necessarily show a considerable slope. Some windows are designed to have a fairly flat and low level of sidelobe peaks, like this three term Blackman Harris window:

This 'minimum 3-term Blackman-Harris' window is defined:

0.42323 - 0.49755cos(2*pi*x/N) + 0.07922cos(4*pi*x/N)

The terms do not diverge a lot from the original Blackman window, yet the result is so different. This really demonstrates the delicate art of window-design. It is not a matter of randomly trying some values! An even more extreme Blackman-Harris window uses 4 terms:

0.35875 + 0.48829cos(2*PI*n/N) + 0.14128cos(4*PI*n/N) + 0.01168cos(6*PI*n/N)

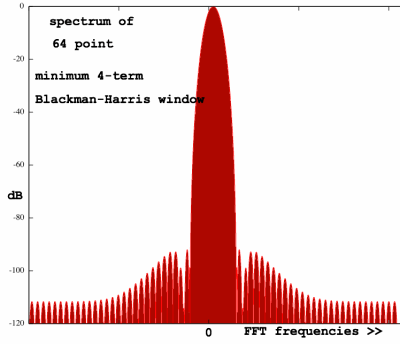I have checked that these Blackman and Blackman-Harris windows give a constant sum with four times overlap, of respectively 1.68, 1.69292, 1.435 to be precise.

I promised to demonstrate phase effects for a modulated window. When a signal is analysed with a windowed FFT, the window is modulated by the input frequencies, or the input frequencies by the window if you want. Positive and negative frequency correlations overlap to a certain extent, and produce phase cancellation / accumulation effects. The effect is best perceived with the rectangular window, as it has the most prominent leakage character. After modulation, the central peak of the window spectrum splitted into a conjugate pair, and the pattern is no longer symmetric round the peaks:

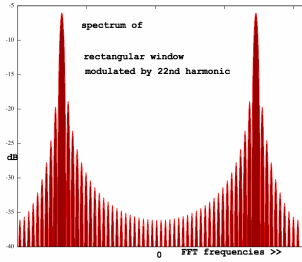We actually see shifted / overlapping Dirichlet kernels on a deciBel scale. With the other windows, like Hann's, the effect is less conspicuous, but it is still there.

window choice

Many more window types are available, and their characteristics can be quantified somehow. I have not tried to do that yet. Above all, I need to know which aspects are important in my case, that is, the spectral filter case. Most texts concentrate on frequency resolution versus dynamic resolution, which is by necessity a trade-off. You can not have a window with narrowest main lobe and lowest side lobe level at the same time. So you choose the window type that best suits your needs.

The resolution question is of concern in analysis and component detection. That is respectable stuff, but what if we want to process the spectrum? What is more harmful: accidentally chopping a main lobe with a Fourier filter, or mowing away the sidelobes that belong to a frequency? So far, I have seen very few comments on this. Of course, if there is a lot of energy stored in sidelobes, a filter would attenuate the wrong frequencies. With steep filter slopes, an amplitude modulation effect can be perceived. How is such modulation generated? I need to know that first, before I could ever understand how to mitigate the effect with a proper window type.