Fast Fourier Transform

On this page I want to figure out a modest example of Fast Fourier Transform. Even for the simplest form of FFT, we need quite some ingredients:

• a standard complex Discrete Fourier Transform matrix, like it is pictured on the previous page Fourier Matrix

• a generic recipe for matrix decomposition, as sketched on the page Sparse Matrices

• roots of unity, roots of roots, roots of roots of roots, as described on the page Roots of Unity

• a method for phase decomposition / interleaving, as explored on the page Phase Decomposition
  

Anyway it is comfortable that I can now recycle some work of the other pages. Here is the N=8 Fourier Matrix, with it's complex entries W^kn computed modulo 8:

We are going to decompose the Fourier matrix into three sparse matrices of the form that was sketched earlier. Recall that these were aggregates of identity matrices at different resolutions. On the left is an aggregate of 16 1x1 identity matrices, in the middle we have eight 2x2 identities, and the right matrix is composed of four 4x4 identities. All these identities must be replaced by W^kn powers. Somehow.

Well for the moment it is better to think in terms of roots instead of powers. My page Roots of Unity demonstrated how a whole set of Fourier harmonics can be generated while multiplying and adding merely the 'octaves', which are related to each other as squares and square roots. This is a phenomenon that we can use for the matrix decomposition.

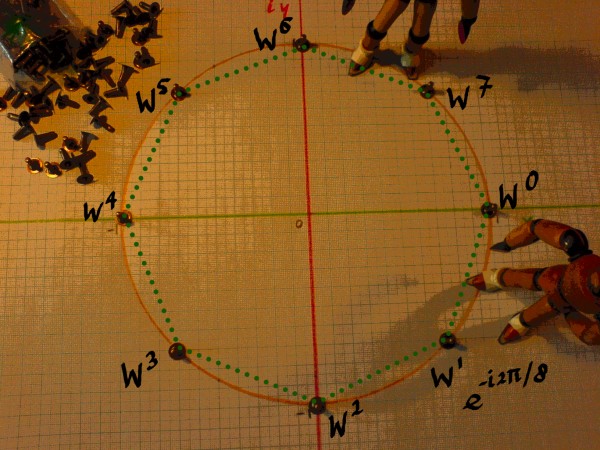
The square roots of unity have W⁰ and W⁴ in the N=8 case, as is shown in the picture below:

The square root of the square root is the fourth root. Expressed as powers of W=e^-i2pi/8, the fourth roots of one are: W⁰, W², W⁴ and W⁶.

Taking the square root of the fourth root we land at the 8th root finally. For N=8, we can not go further than this.

On the Fourier Matrix page the sine and cosine series for these cases were plotted. I put those plots together here:

Samples of the square roots of unity

Samples of the fourth-roots of unity

Samples of the eight-roots of unity

There is still one important series missing. It is the first root of unity, or 1^1/1, and it's powers.

That sounds quite trivial indeed. But the fact that W⁰ operates as an identity follows from our definition of W as being a complex root of unity. I feel we should remain aware of that. W⁰ is the most-present root in the Fourier matrix. It's power series dominates the FFT. The series forms an identity with respect to rotation. It is a conservator of frequencies.

Samples of the first-root of unity

Let us look at the W^kn matrix once more, and confirm which harmonics we are going to use, and which ones are skipped:

The question is now, how are we to arrange these frequencies in our N=8 sparse factor matrices? Sure this can be derived from the DFT formula, using a sequence of equations. These are fairly complicated however, and I always lose track at some point when studying them. Otherwise, there are these butterfly schemes that accompany most texts on FFT. But I am not a fan of that either. Maybe it is an idea to translate an FFT butterfly scheme to a matrix representation.

To find a suitable scheme I studied more butterflies than I ever wanted to see, none of them being precisely what I needed. I sort of distilled a form that will serve the purpose of this demonstration. Here we start with the first sparse factor, containing first roots of unity in the upper part and eight-roots of unity in the lower part:

When we consider the next sparse factor as a repetition of the process at another resolution, then we see the W⁰ series on top again. Powers of W² are in the lower halves. W⁰, W², W⁴ and W⁶ are the fourth-roots of unity here.

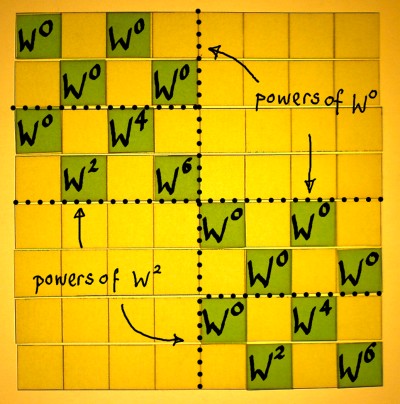And here is the third sparse factor, it is the last one for the N=8 case. We find the W⁰ and W⁴, square roots of unity, in the lower parts of the small submatrices.

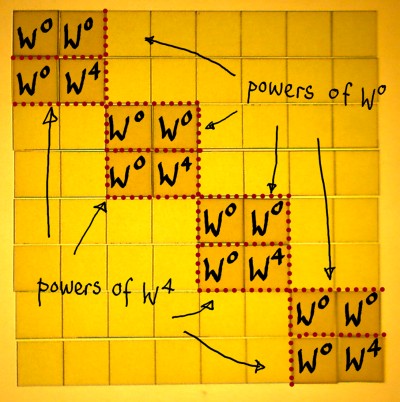For convenience, the three factors are pictured together here:

From these matrices, you could already have the impression that it will split output results into smaller and smaller vectors in every stage. The upper half of each submatrix has merely identities summed, while he lower half has rotations.

Let us now verify whether these sparse matrices multiplied will really render the complete W^kn matrix. First multiply B with C to get BC.

Then multiply A with BC to get the full matrix ABC:

Some of the entries have exponents above 7, and these are to be computed modulo 8. Below we have ABC in a form which can be compared with the W^kn matrix. Hey, it is interesting: all harmonics are present in ABC, but they appear in the wrong order. Actually, they appear in so-called bitreversed order.

If you would use the sketched FFT factors for correlation, the spectrum would appear in decimated or downsampled form. The decimation is an inherent aspect of this FFT process. It happens stepwise: a factor 2 downsampling in each stage. The most efficient solution is to just let it happen. At the end of the process, it can be compensated with a bit-reversed permutation operation, if needed.

Bit-reversed permutation does in one operation what even-odd decomposition does in several stages. By the way, total decomposition, total interleave, and bit-reversed permutation all have the same effect. A bit-reversed permutation operation is illustrated here, with the indexes of the matrix written as binary numbers:

The Fast Fourier Transform as sketched on this page can easily be expanded to larger N, if only N is a power of two. It is a radix 2 FFT. Radix means base of the numeral system, and it is the Latin word for root. Radix 2 is only one of the many options for FFT, and even for radix 2, different schemes are possible. I am not going to discuss these alternatives yet, because we are not even ready with our simple example. It can be further decomposed, increasing efficiency one more time. That is for the next page.